Overview
The overall purpose of the project was to learn about the physics simulation of cloth and how it interacts with materials in the physical world. In simulation, this is modeled using forces, masses, and a sheet of independent springs that represent the relation between particles within a cloth. It was quite interesting to see how the cloth interacted with objects based on object type (sphere or plane), and how the cloth folded when we added new functionalities including self folding. Furthermore, it was neat to see how varying parameters changed the results. For example, we could change the spring constant, and it would be similar to modeling different materials of cloth. We could vary the forces acting uniformly on the object, like adding gravity, reversing gravity, and other things like that. My approach was to make sure I understood the object, reference, and pointer types we used throughout the project, and to ensure that all the iterations over the point masses or springs did their jobs of applying the necessary actions over the entire scope of the simulation.
Part 1: Masses and springs
In part 1, we initialized a grid of springs and masses to represent a discrete representation of the cloth. Given parameters like the number of points in width and height directions, we made the representation of cloth similar to a plane, except made of independently acting points that could deviate from the plane. After uniformly initializing the point masses, we added springs to model constraints that existed between the point masses on the cloth. The three constraints we modeled were the structural, shearing, and bending constraints. Shearing constraints were diagonal while structural and bending were both only up and down, and left to right.
|
|
|
|
Part 2: Simulation via numerical integration
In part 2, it was our job to implement the forces that would be acting on the point masses by both the external forces and by the springs representing the constraints between point masses. The first force we applied was the total external force. This was computed by summing all the acceleration vectors acting on every point mass, and multiplying by the mass to obtain the force. Force = Mass * Acceleration. Then, for each independent point mass, we calculate the force applied by the springs/constraints acting on it. The force of a spring is computed by the displacement * the spring constant. We use all of the forces to compute a total force vector on the point mass.
The next step was using Verlet integration to compute the new positions of the point masses in our cloth. In this version of integration, we approximate that velocity * dt (the timestep) = the displacement between timestamps. We use the damping term and calculate the new position of the point mass as a function of the acceleration applied and the original displacement (now velocity). The final step of this part was to constrain shifts in the displacement to prevent extreme shifts occurring near the pinned points. Examples are demonstrated in the images below. The constraint was defined as 1.1*rest_length to represent that cloth does not actually stretch as sharply as the simulation might have once suggested.
Pinned 4 in various states:
|
|
|
|
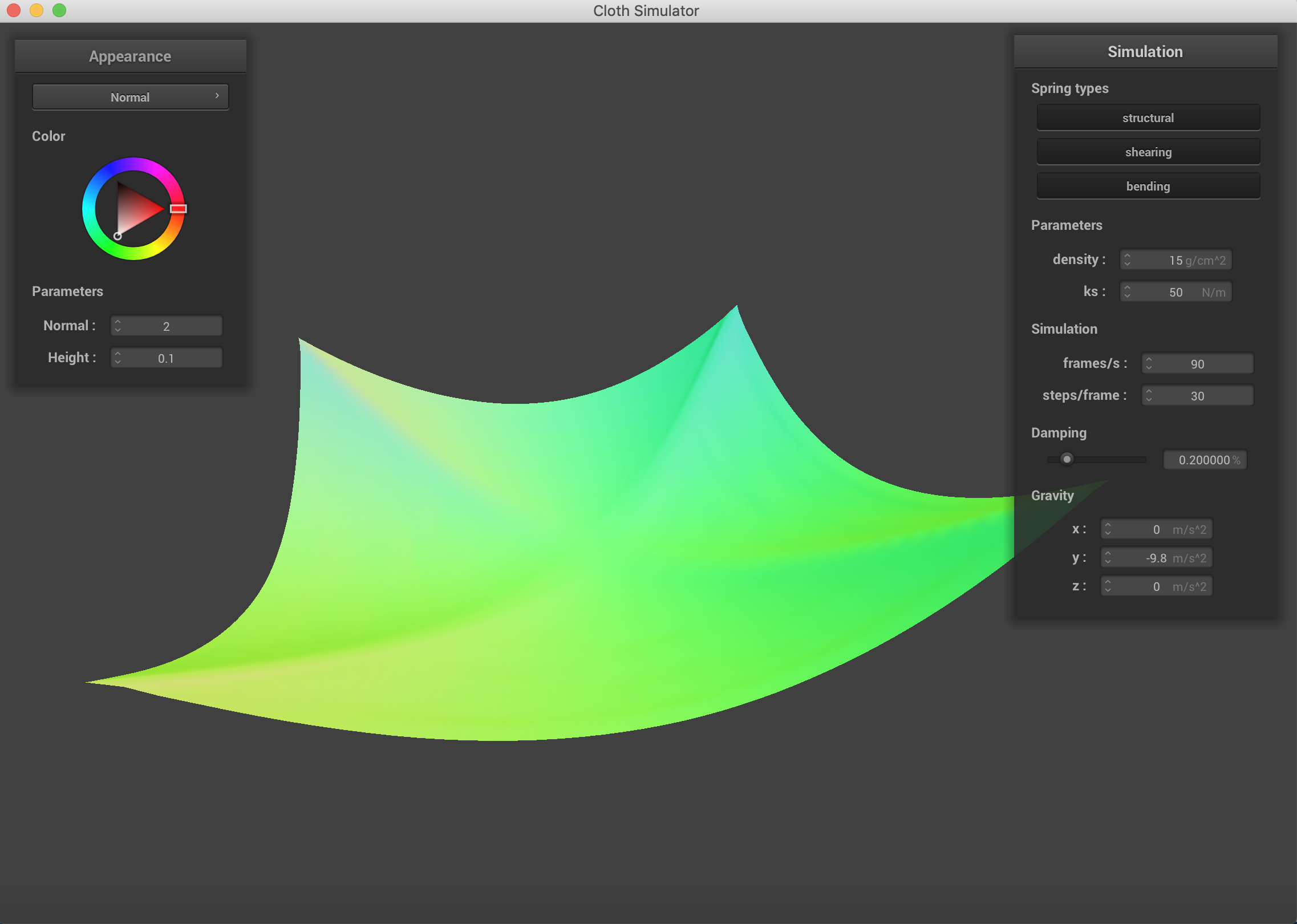
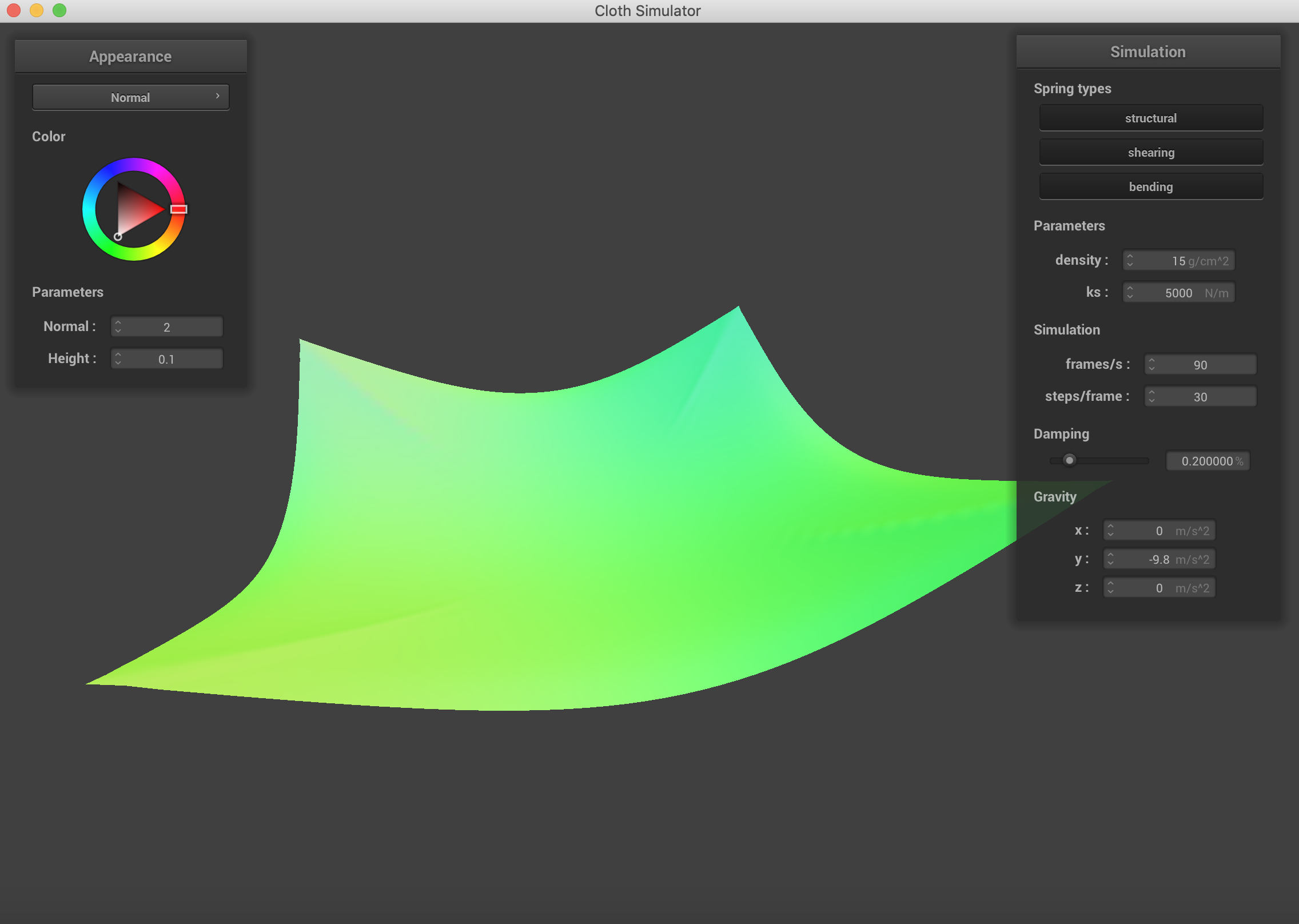
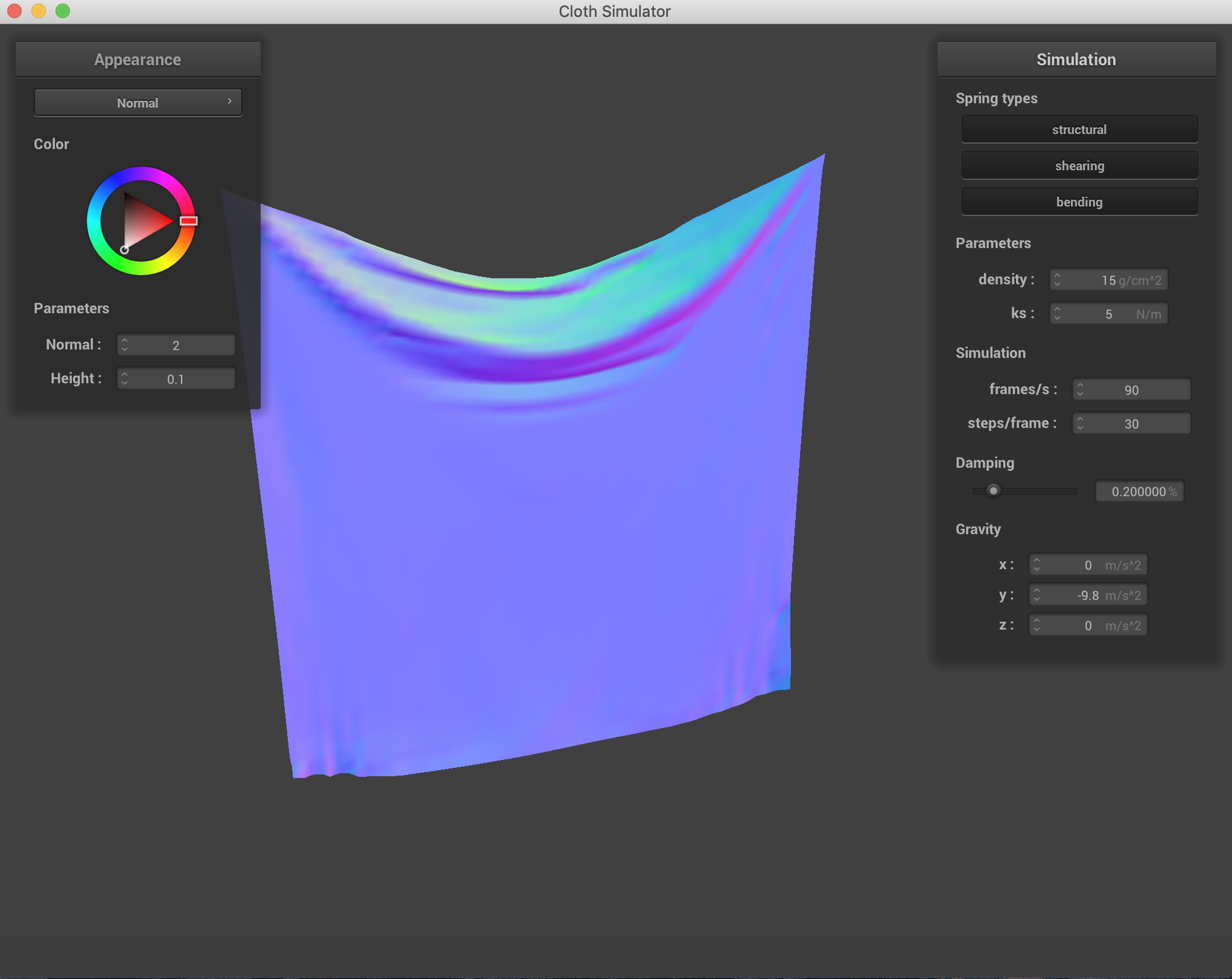
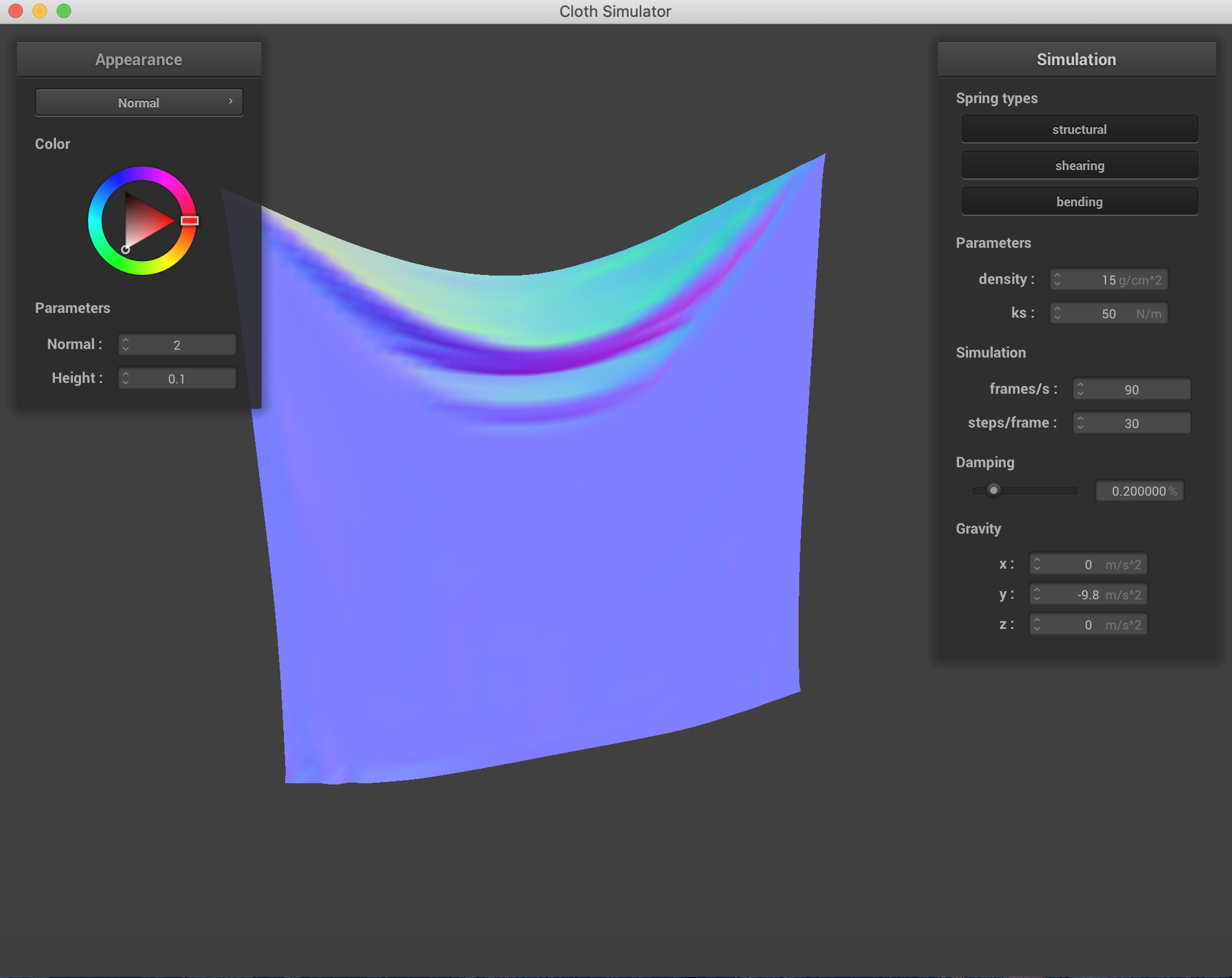
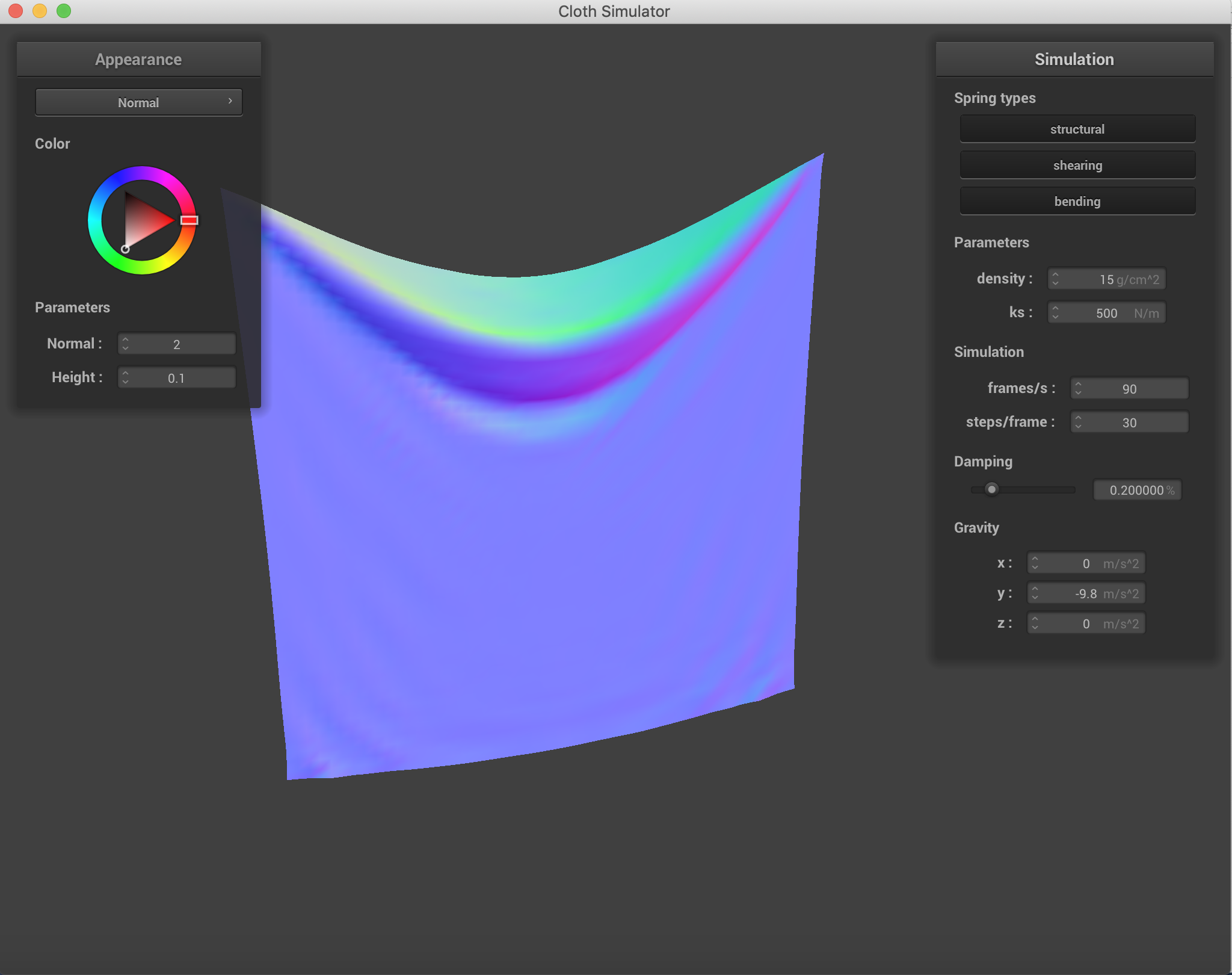
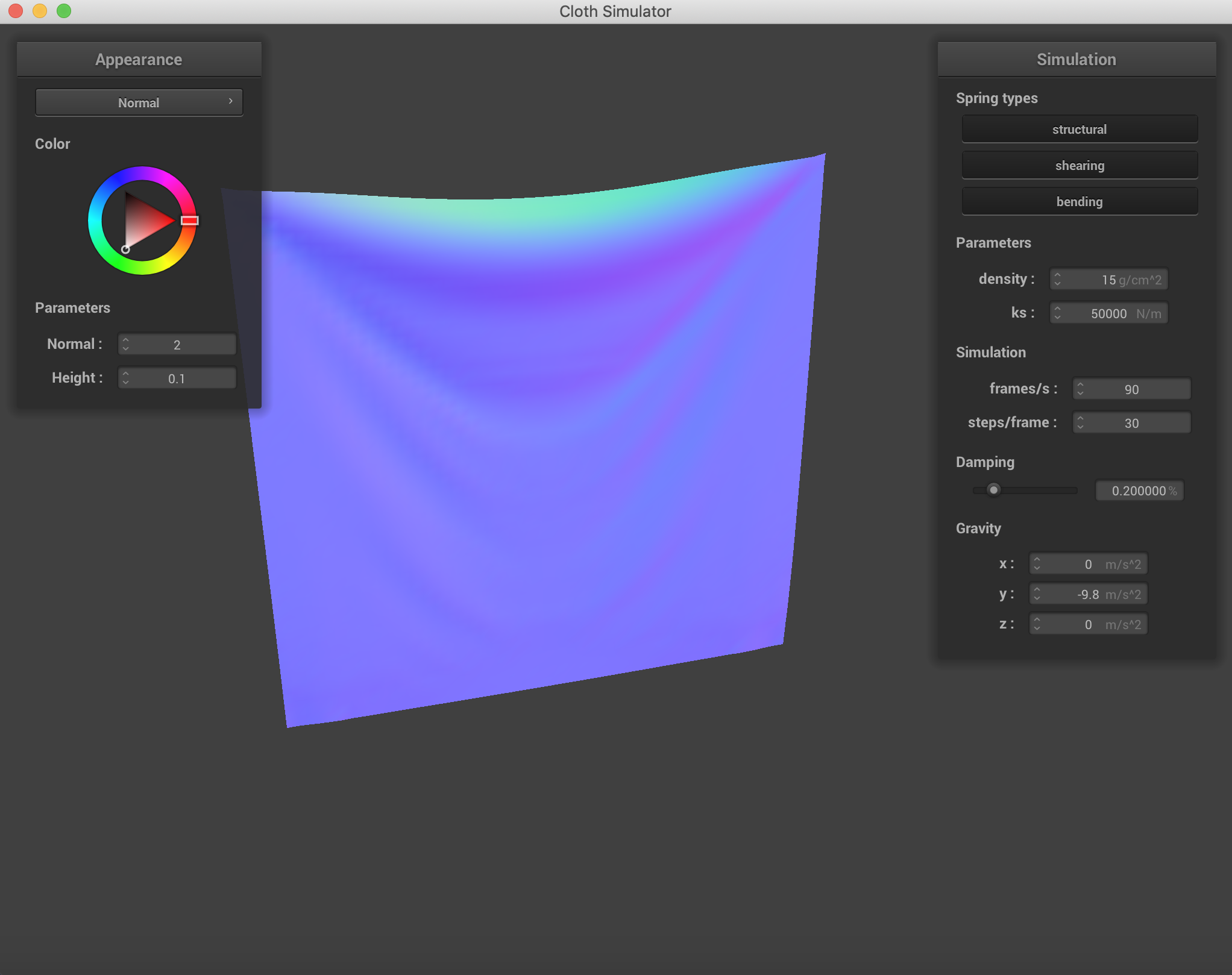
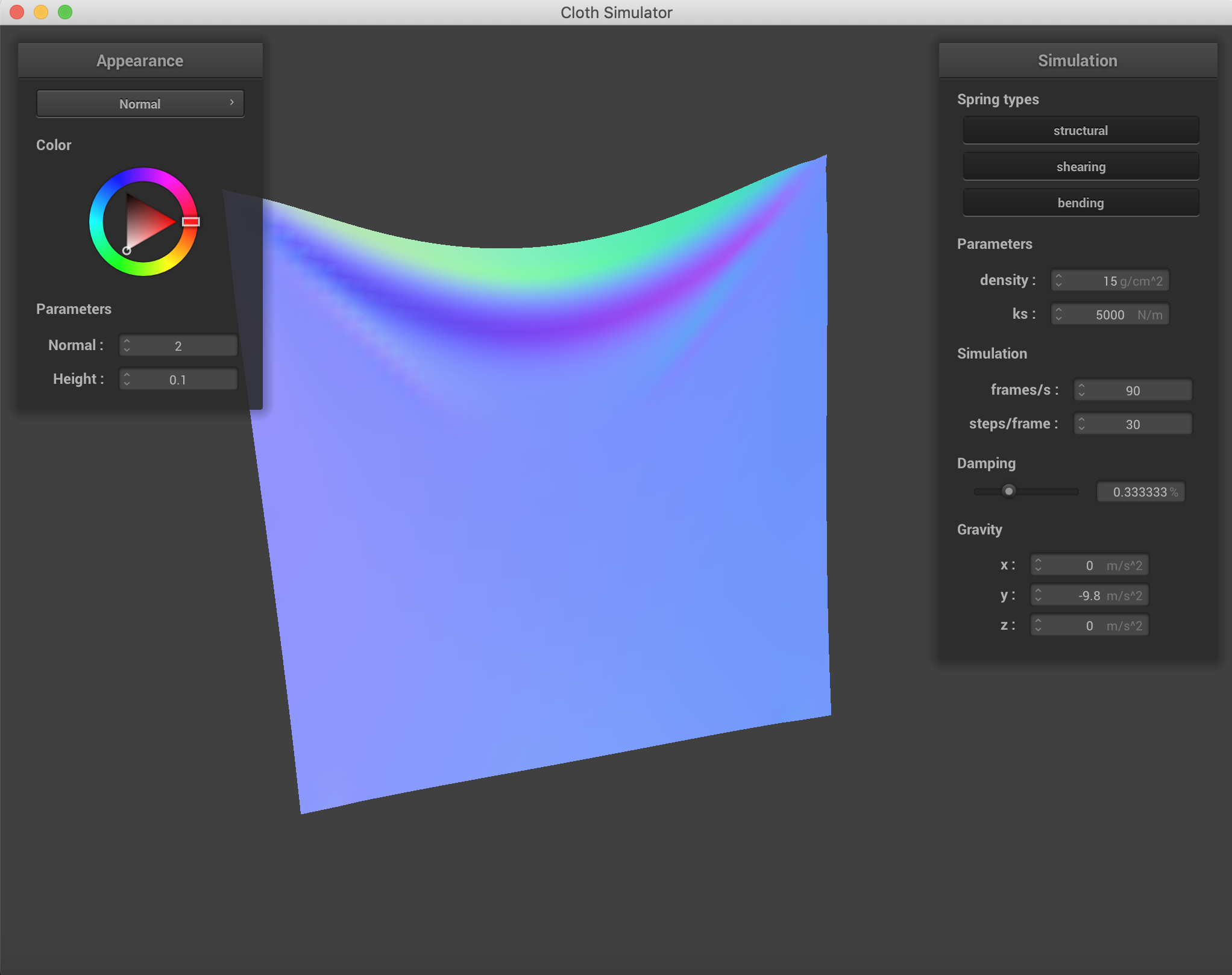
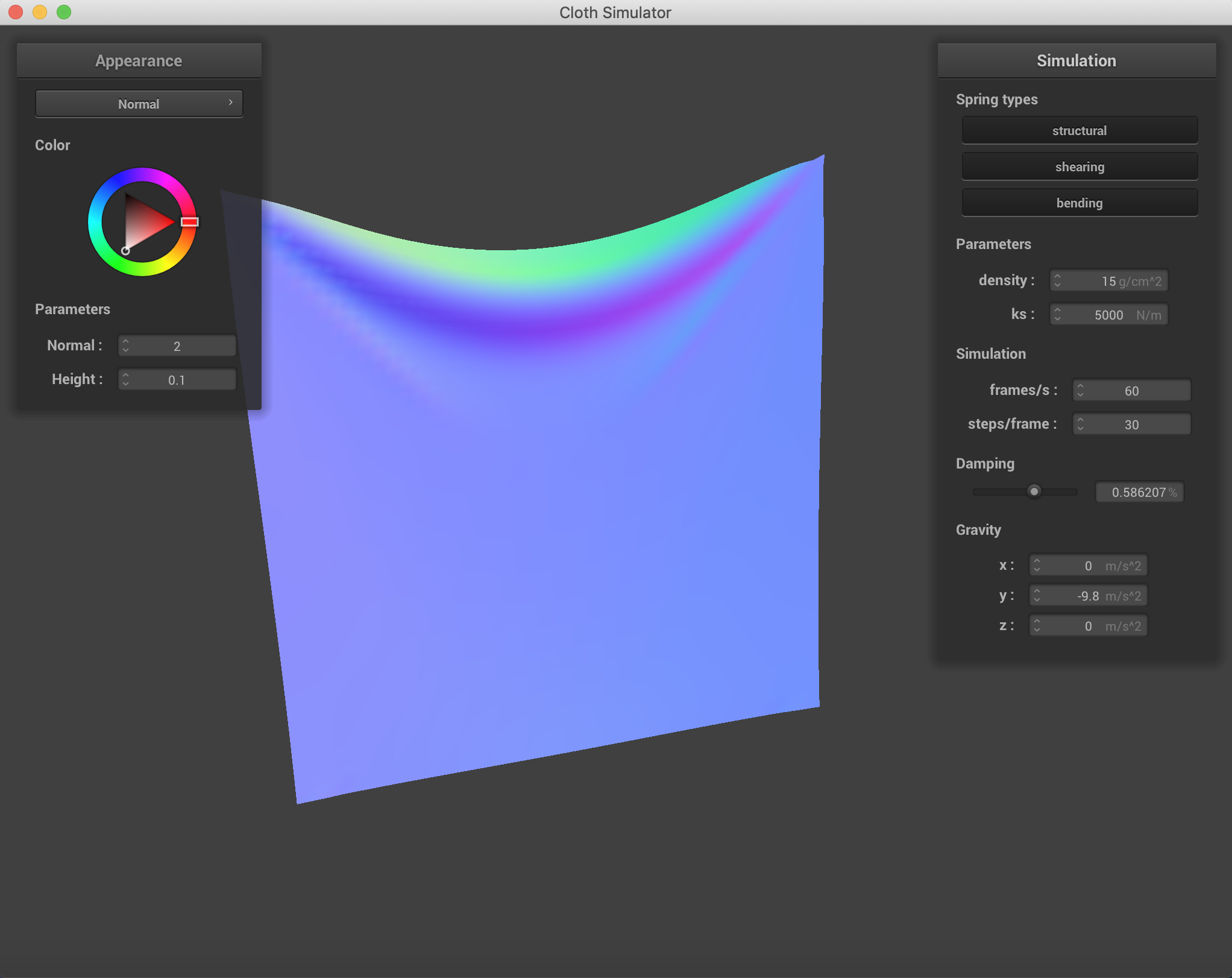
Changing which constraints are being used on the cloth. Density = 30 g/cm^2, ks = 500N/m. It is clear to see that using all three constraints simultaneously is the best representation of what the cloth actually looks like after falling.
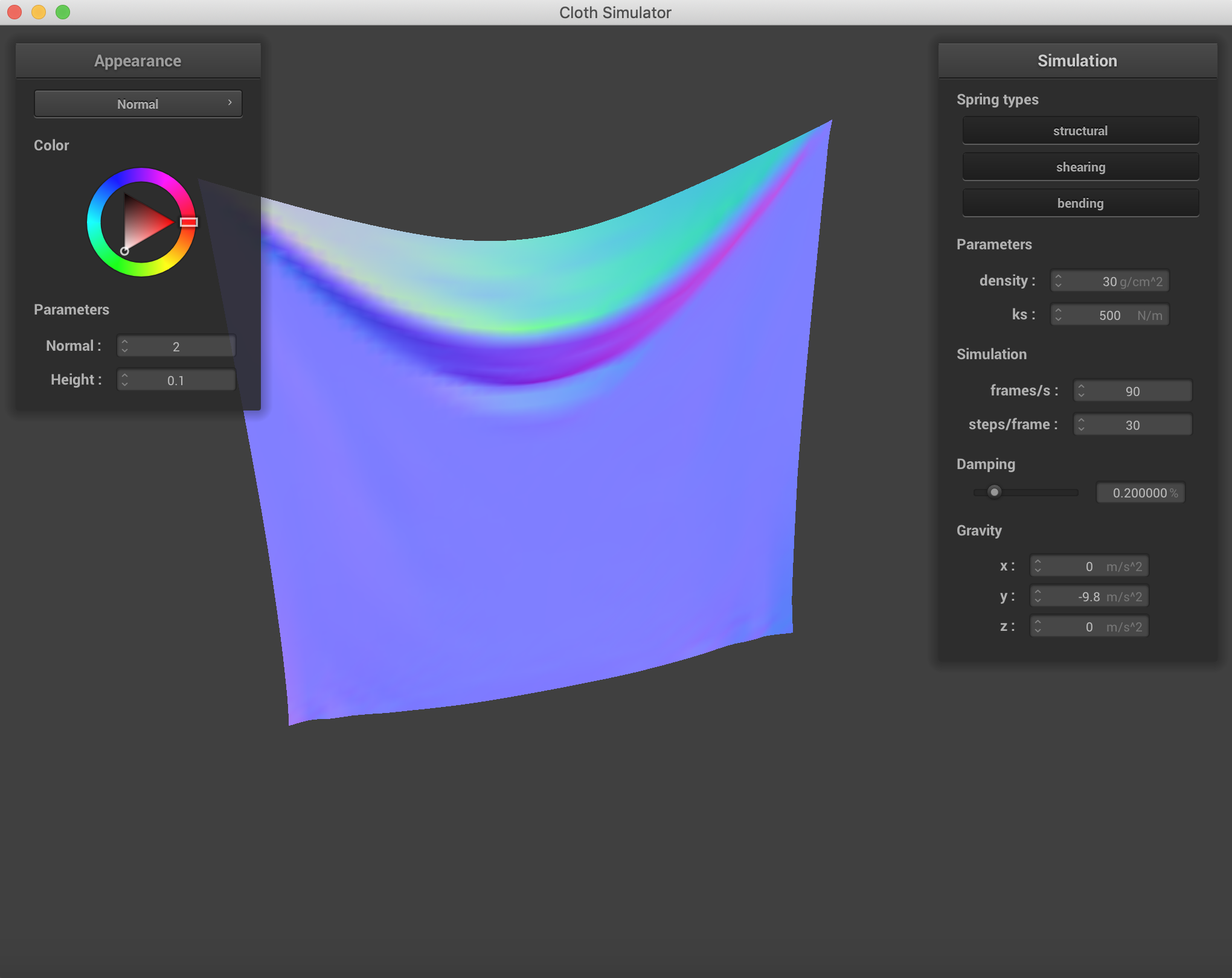
|
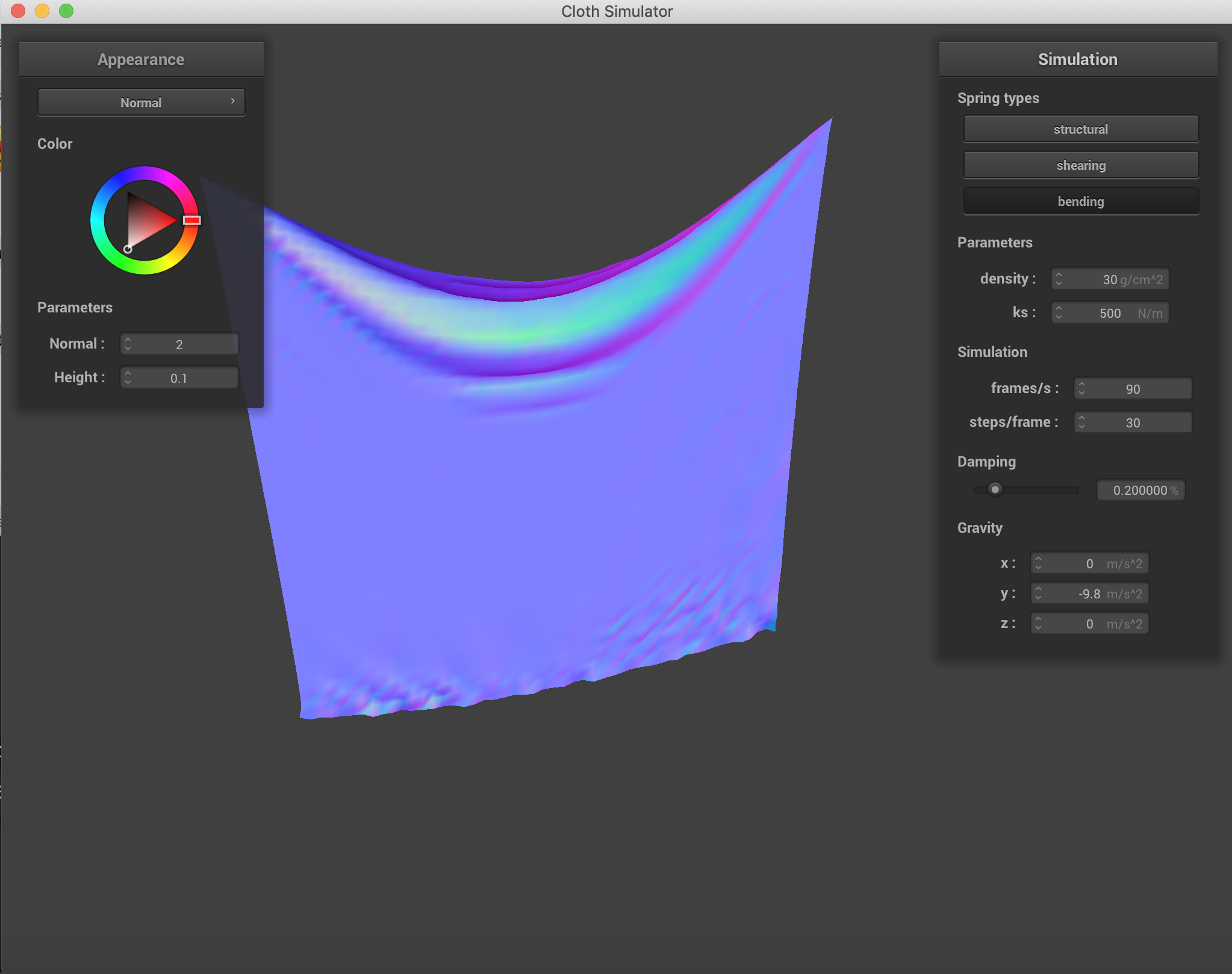
|
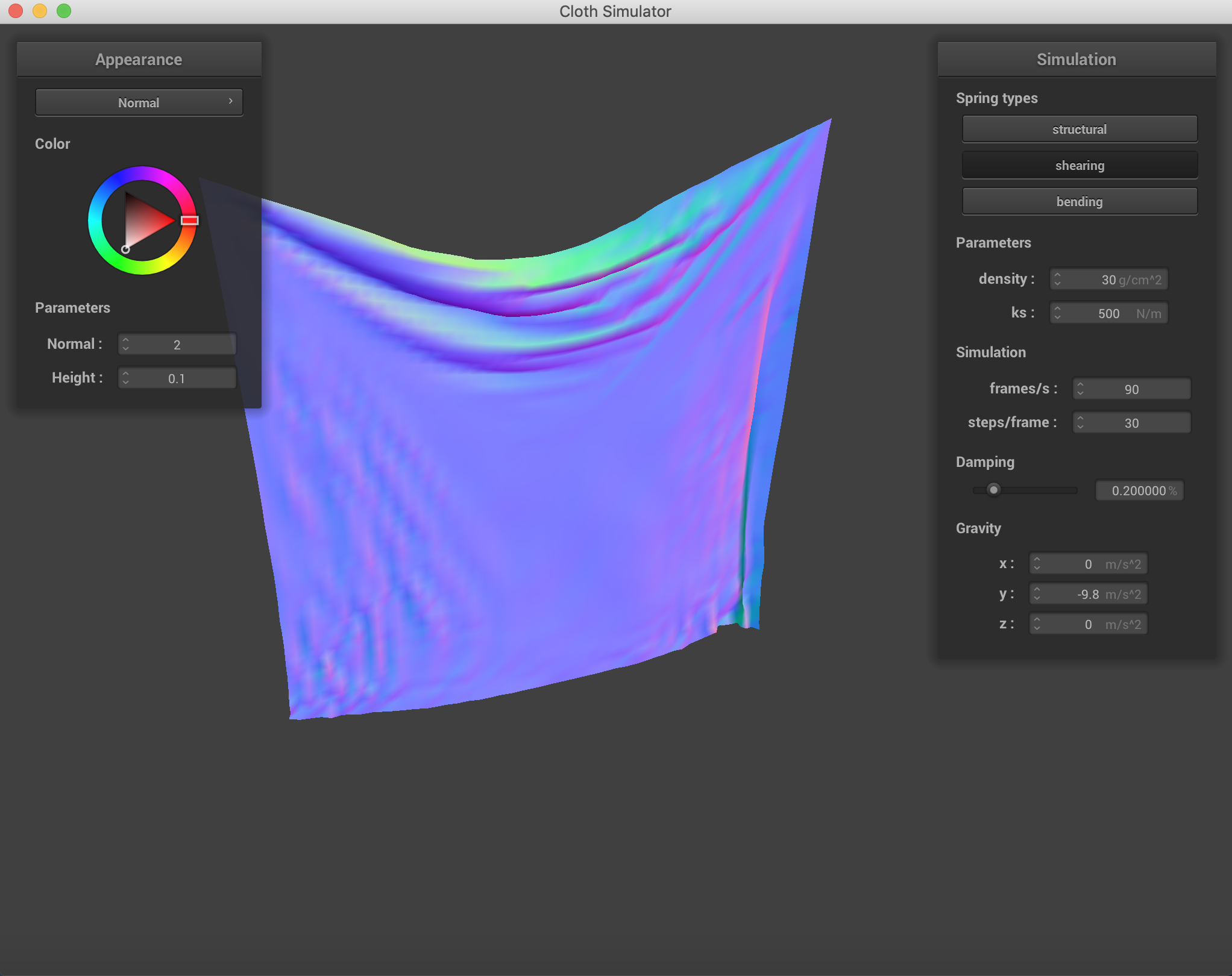
|
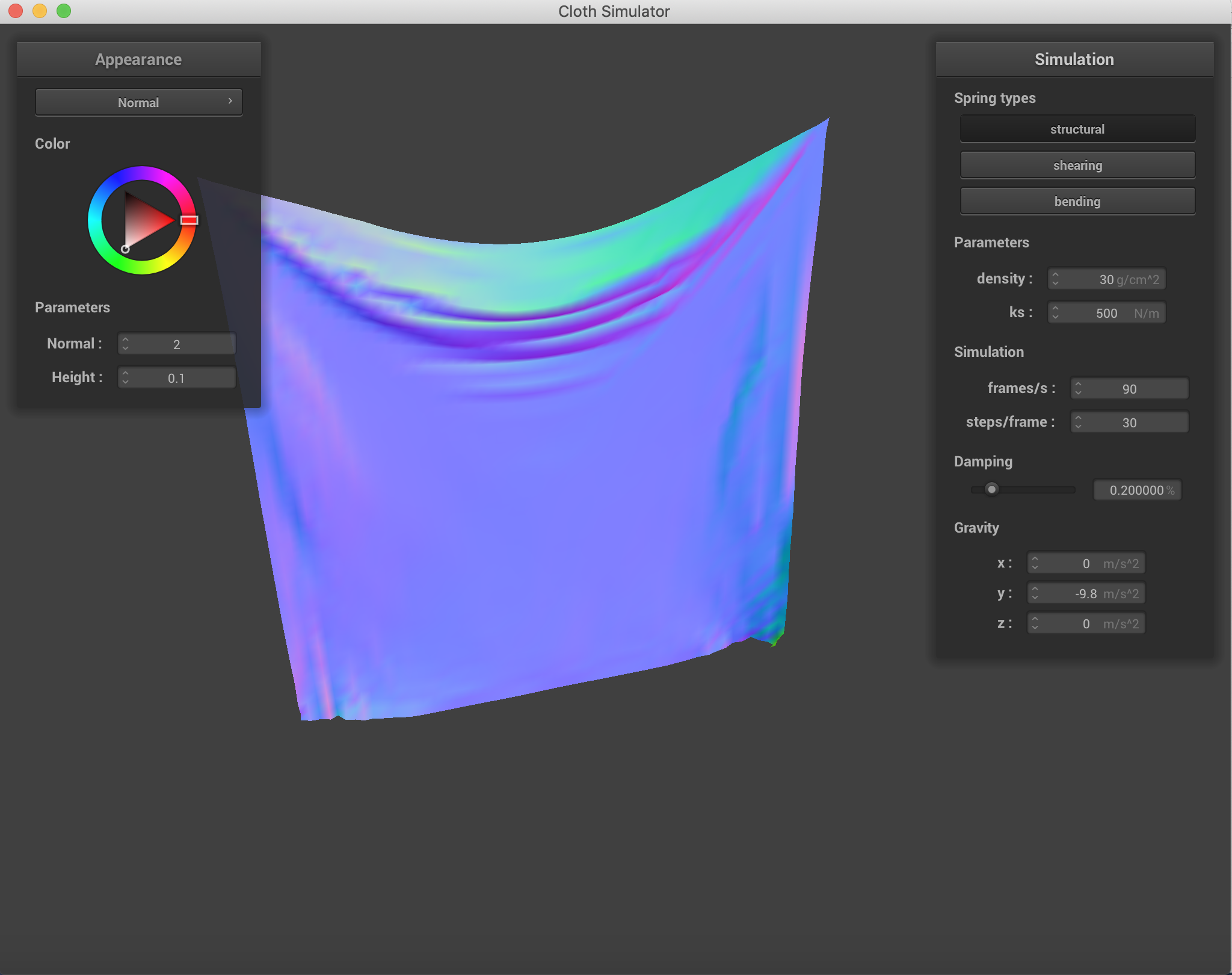
|
Various other parameters and configurations.
|
|
|
|
|
|
Mostly with damping, the speed of falling on the cloth was affected more than the end result. The change in spring constant was incredibly visible with the way folding happened and the end formation and the "strength" of the cloth. When damping was low, the uniformity was lost across the falling of the cloth. And when damping was higher, the cloth fell rather stiffly.
Part 3: Handling collisions with other objects
In this section, we implemented planar and sphere intersections. It was actually not as difficult as anticipated. Instead, the only trouble came with manipulating the vectors to get the correction vector. Applying magnitudes in directions is very easy given the Vector3D representation. To find out if a point was in the sphere, I checked against distance from the origin and the radius of the sphere. For the plane, I checked if the position and the last_position were on different sides of the plane using the dot product of the point with the normal vector and comparing signs. The point of tangency was determined using point projections onto the plane, and then the correction distance was straighforward. The surface offset was also used to prevent small errors in the form of intersecting across very fine points when intersecting with what is essentially a two dimensional plane.
On the left, there is an example of one of the error outcomes that I thought looked really cool. On the right is the correct version of the deliverable.
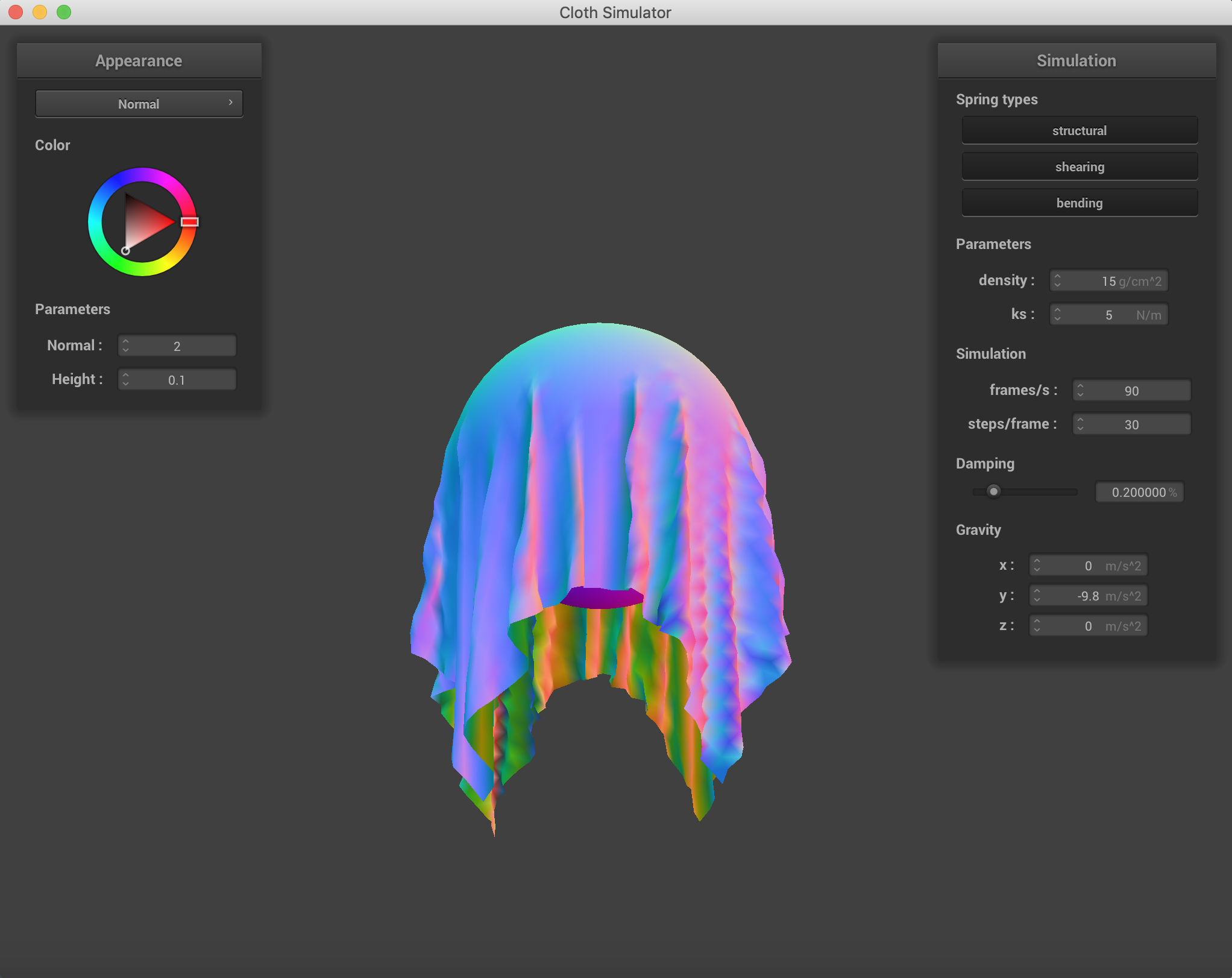
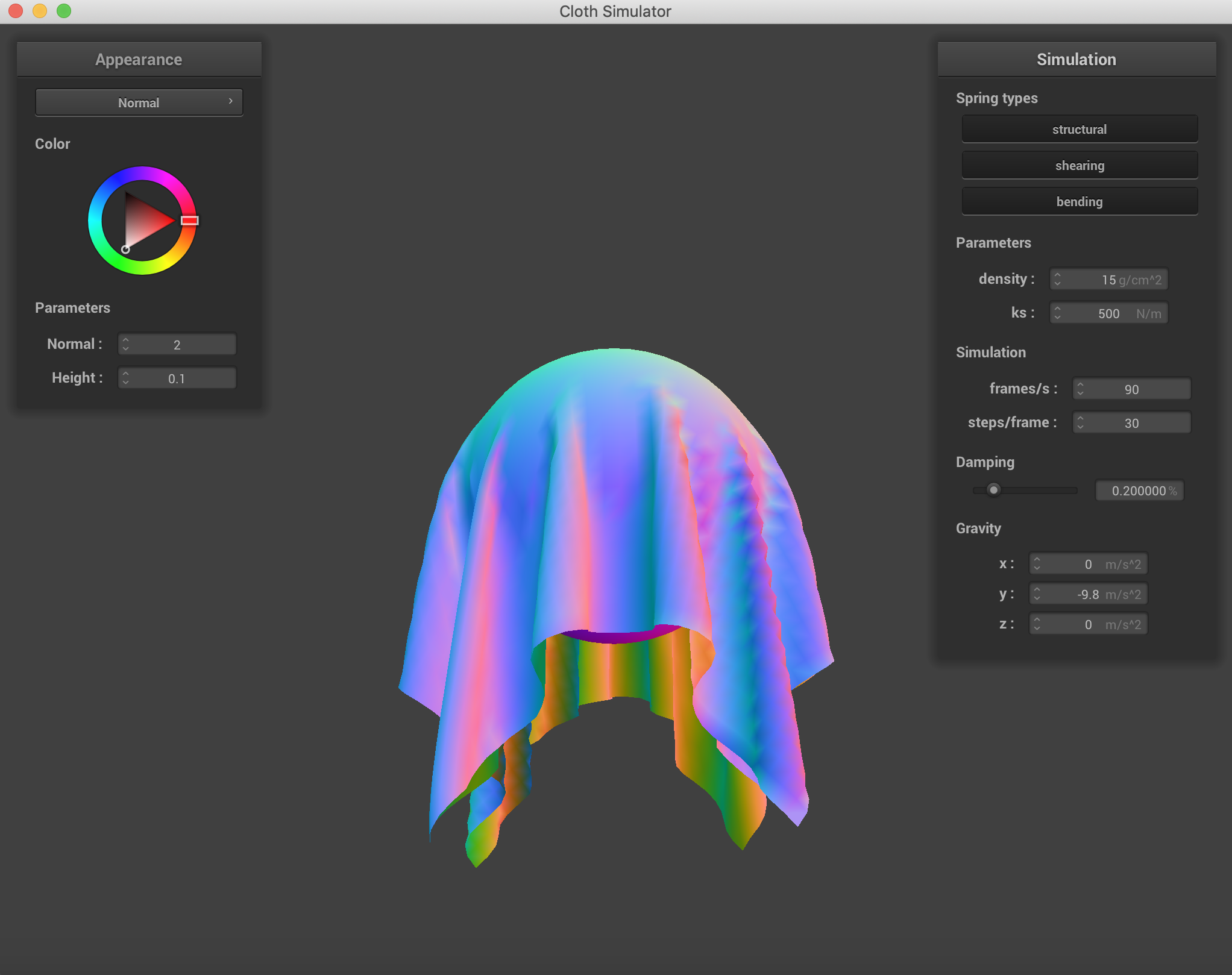
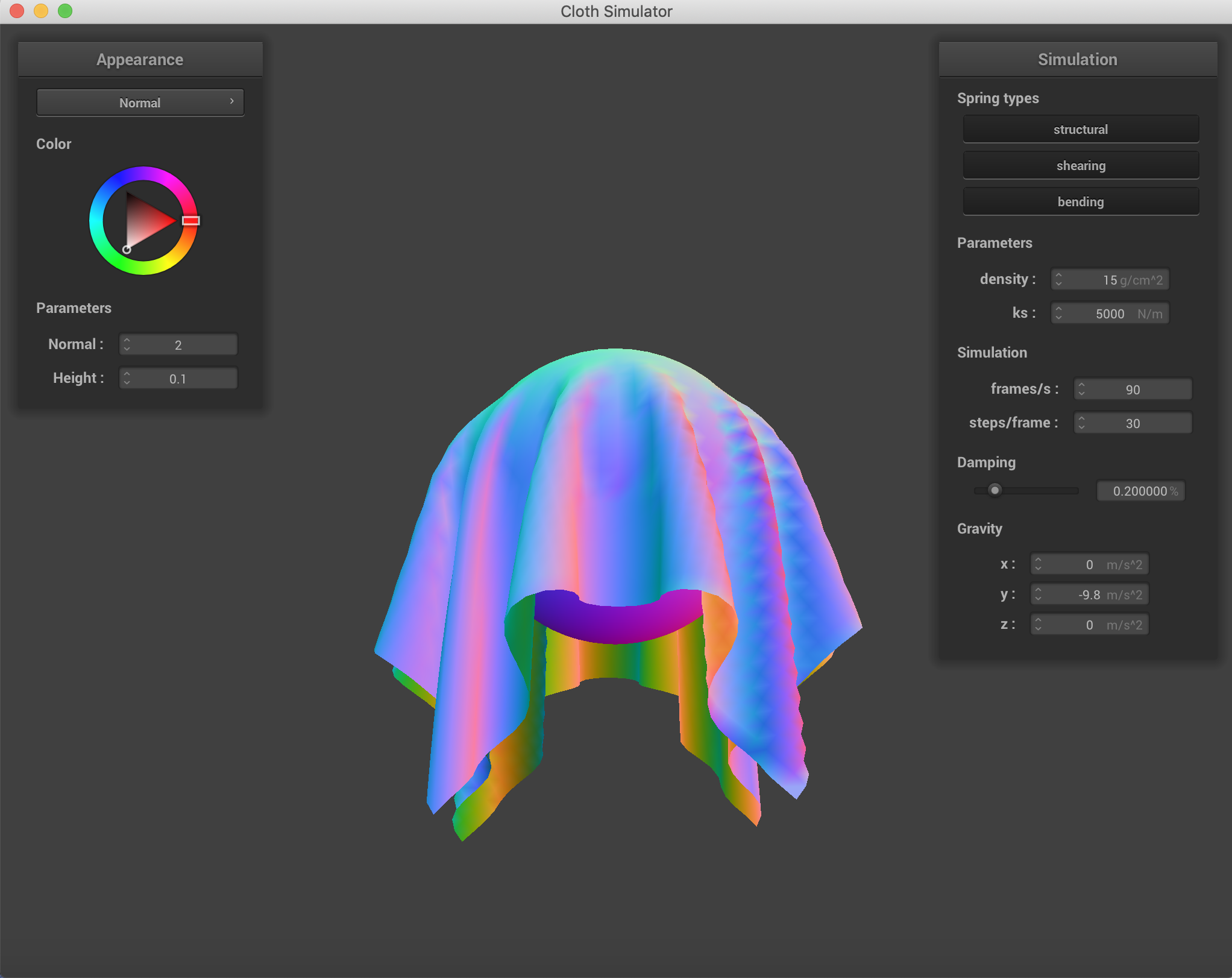
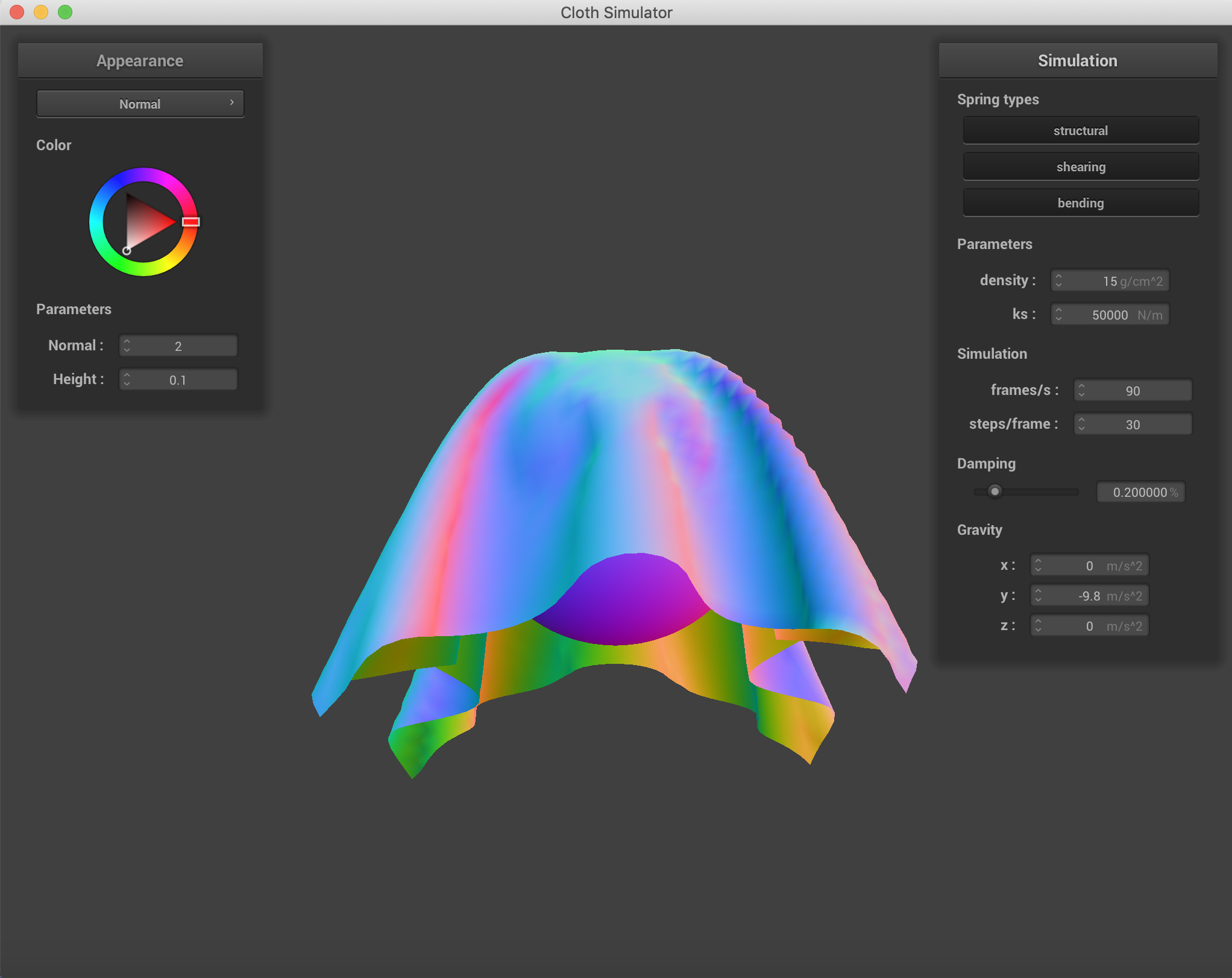
The Spheres with various spring constant values. As the spring constant went up, the cloth doesn't quite wrap around the sphere as much and there is more force being applied on the point masses by the corresponding springs, because the spring equation has force being a linear relation to the spring constant. Adjusting damping changed the way the cloth fell onto the sphere and the stiffness with which it folded.
|
|
|
|
|
|
Part 4: Handling self-collisions
To handle self collisions is actually a computationally difficult task because it involves checking each point mass with every other point mass to determine whether or not an intersection has occurred. This is an O(n^2) relationship to the number of point masses representing the cloth. However, we can narrow down the potential for intersections using a bounding box and a hashing method.
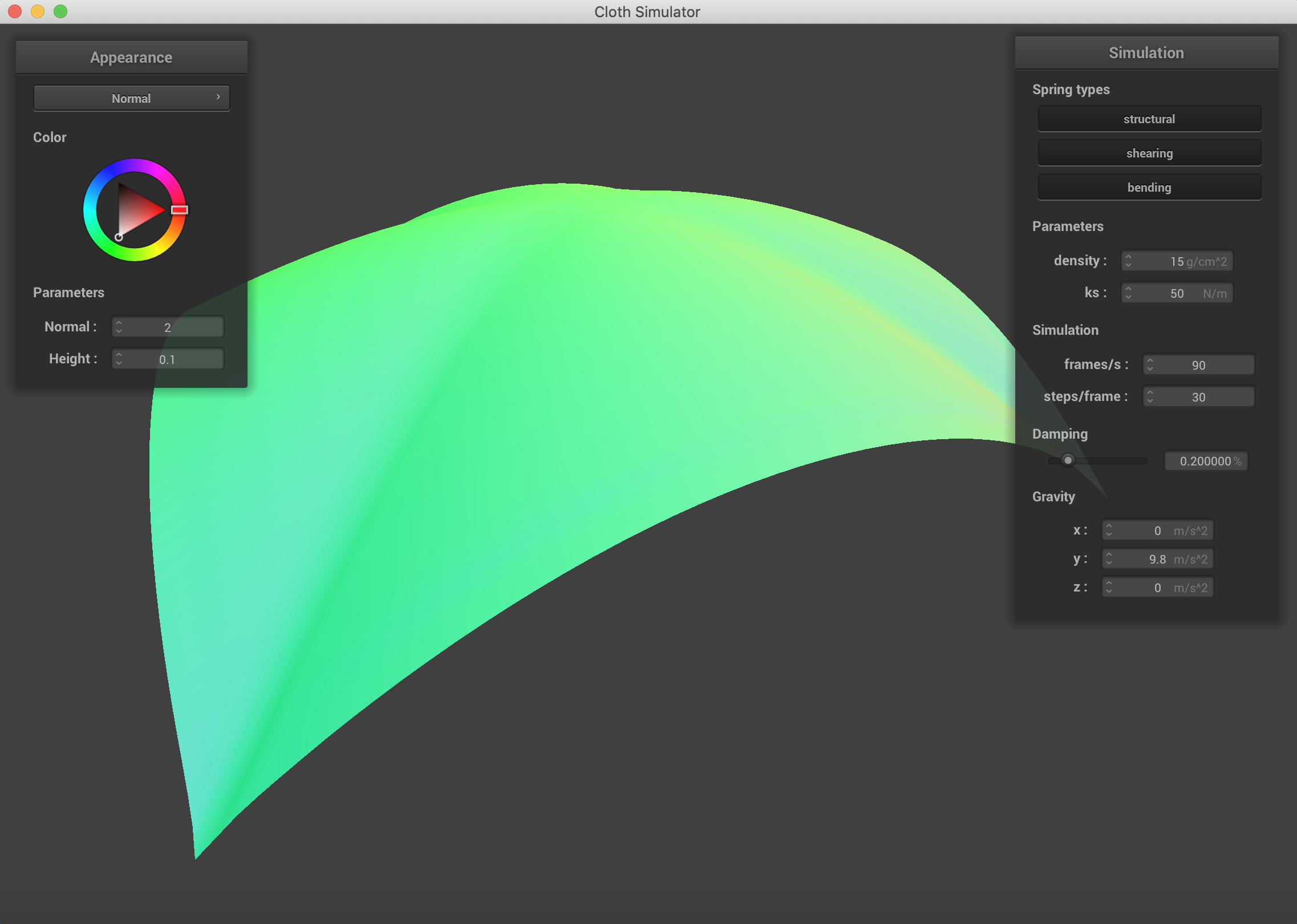
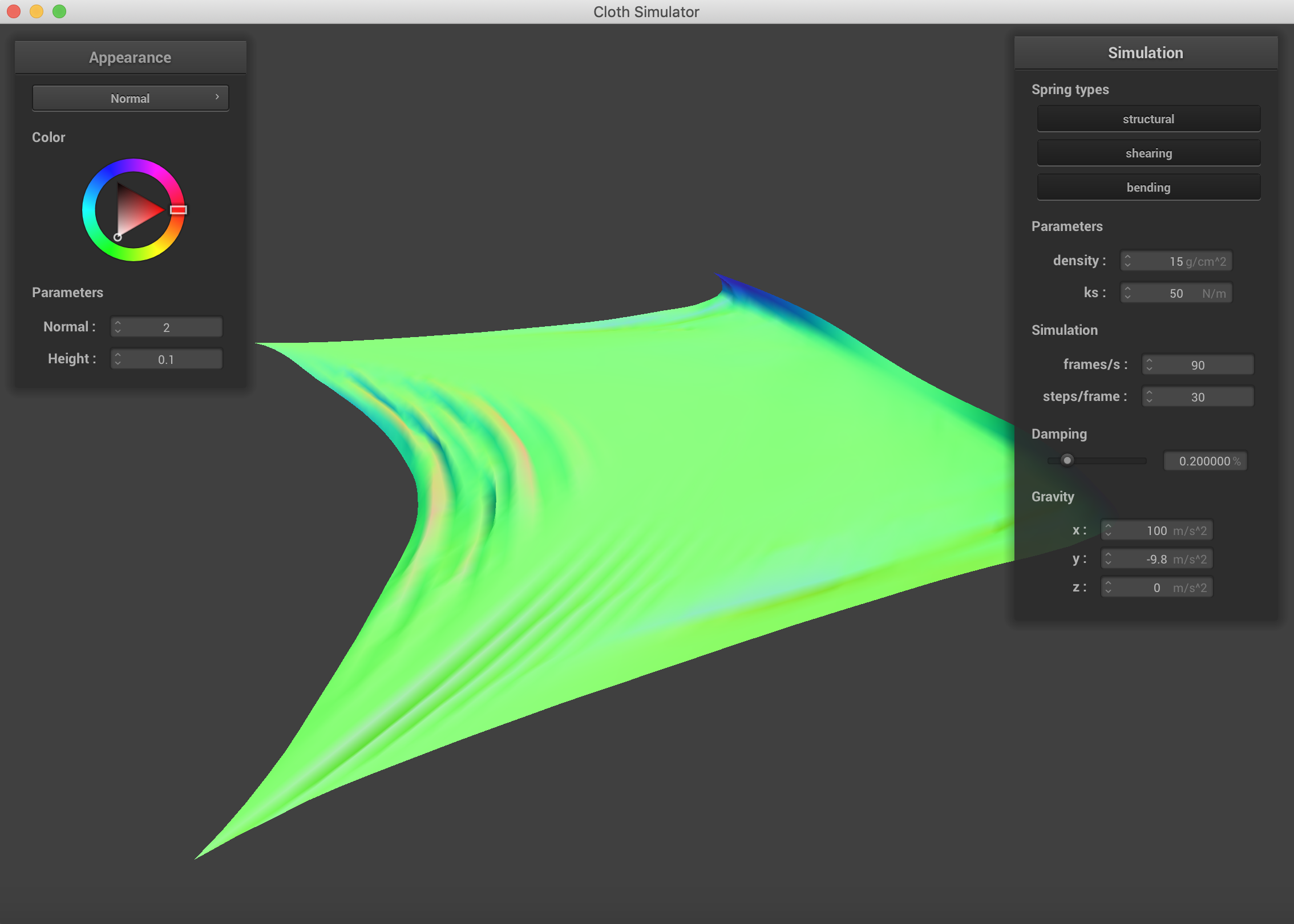
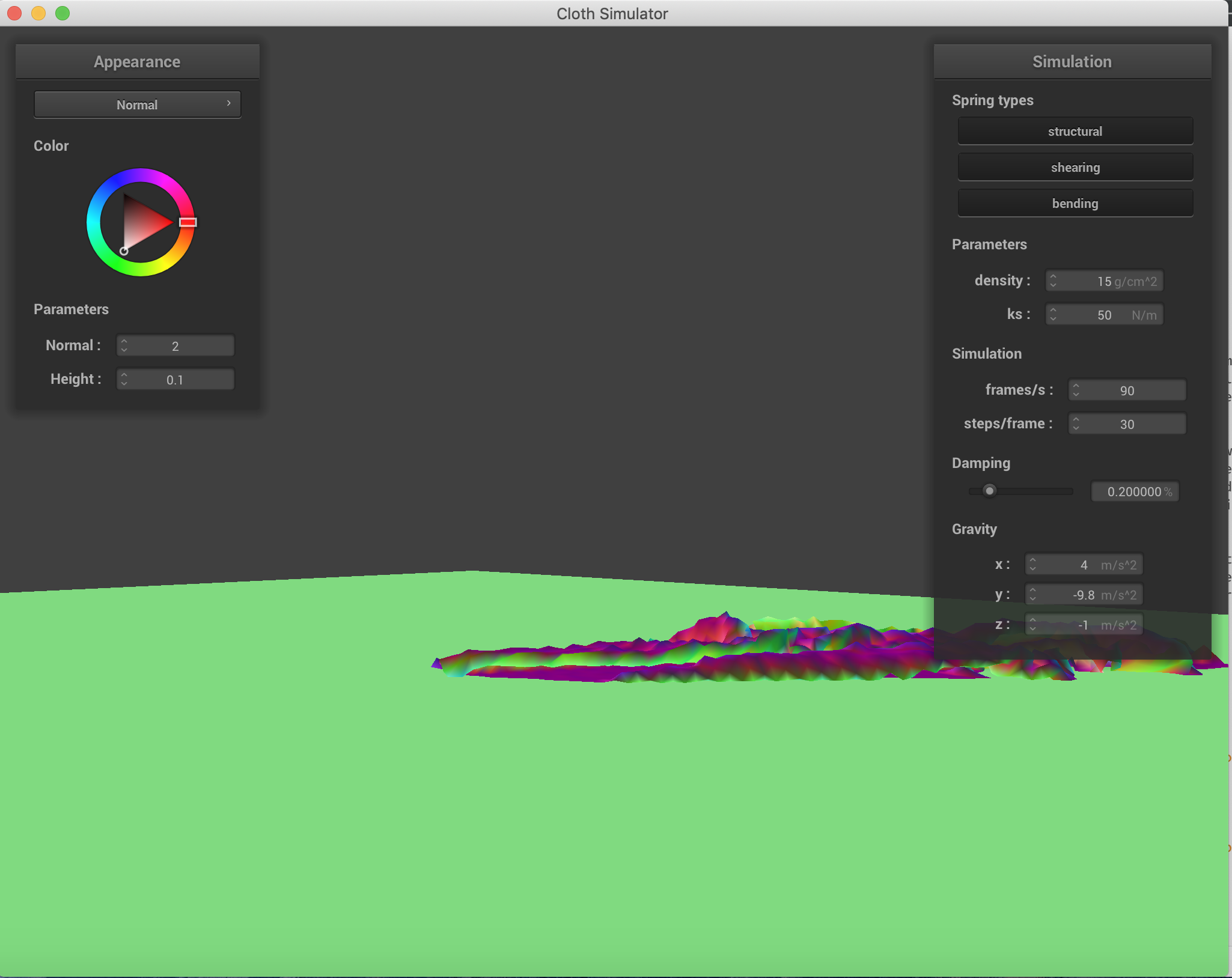
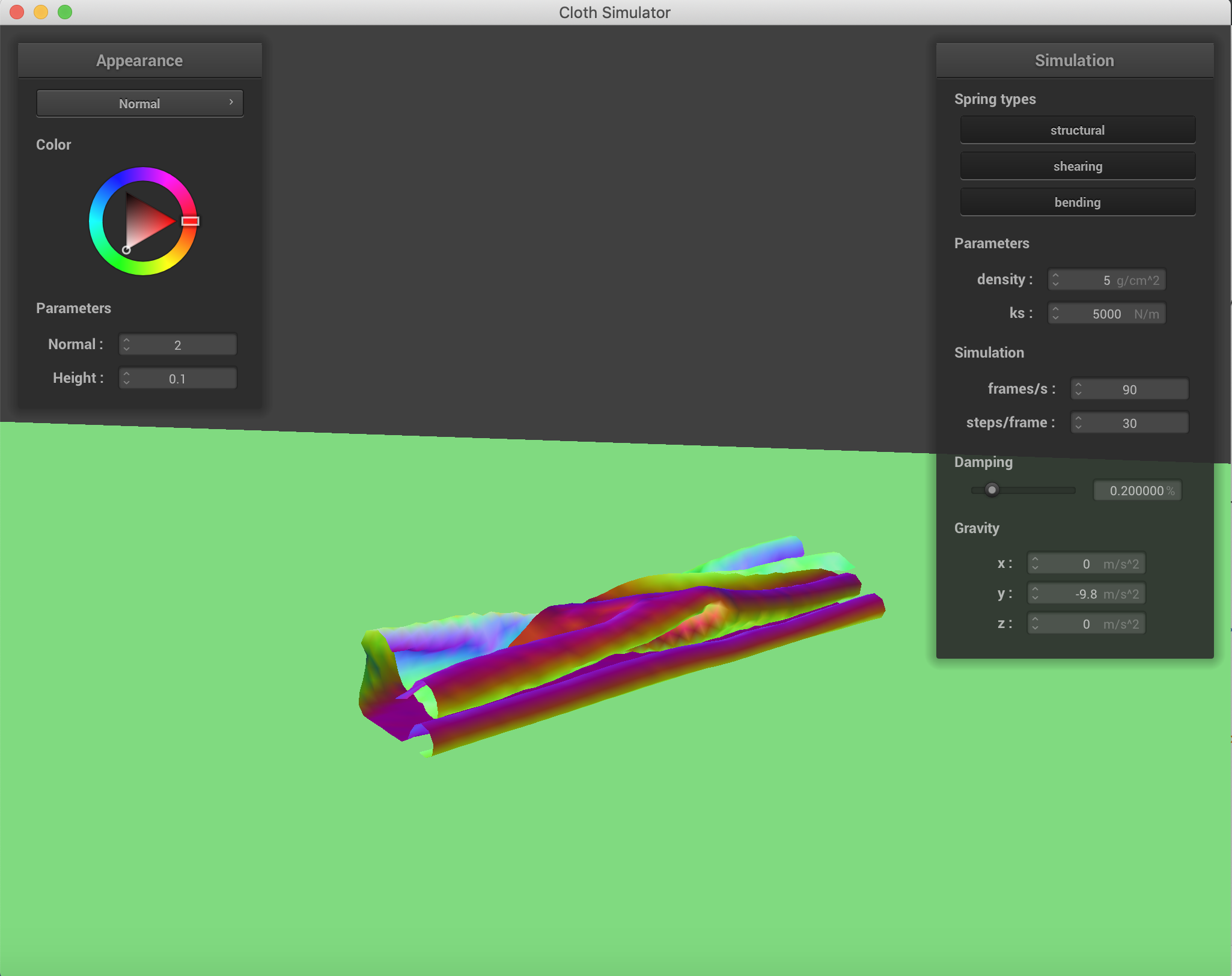
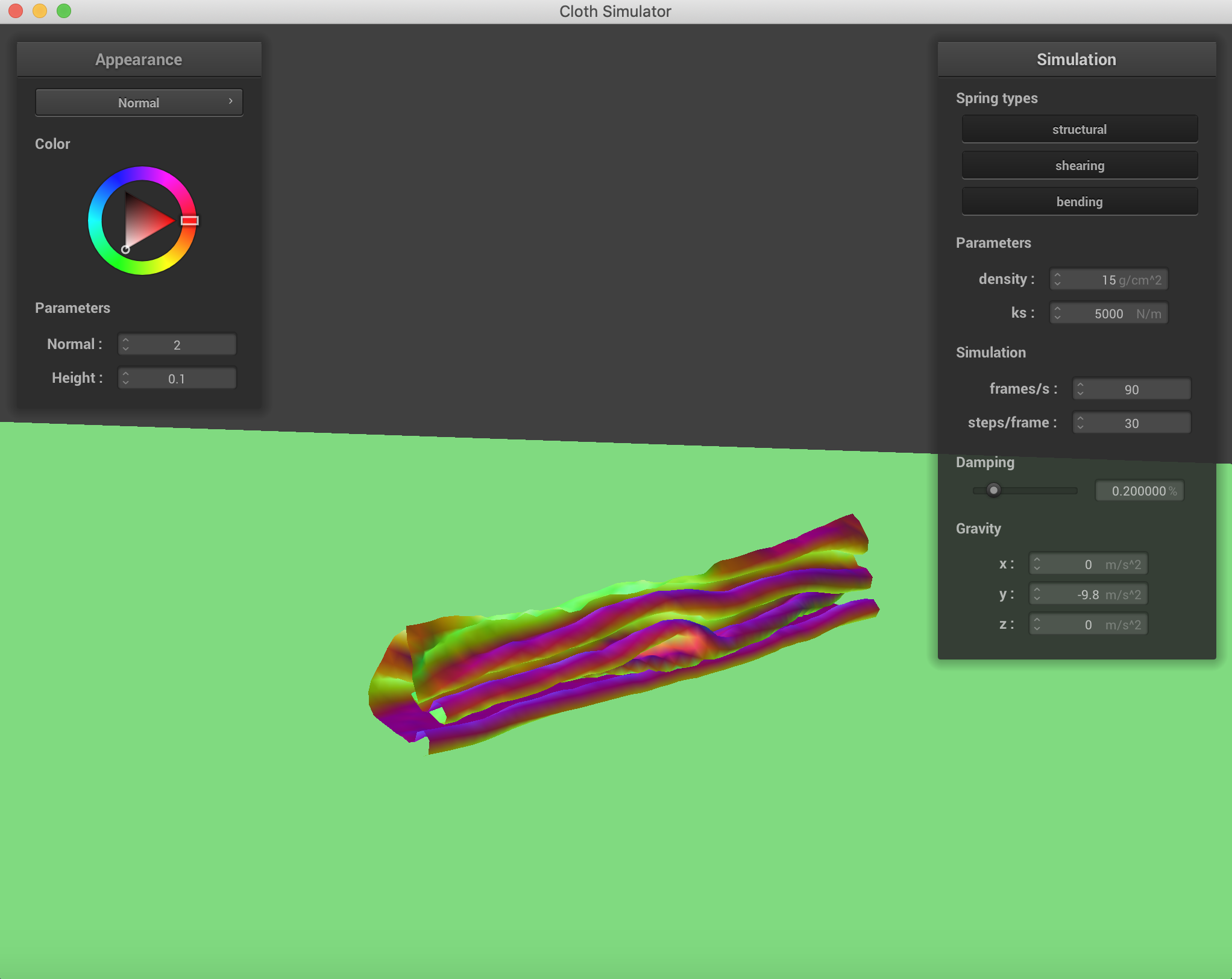
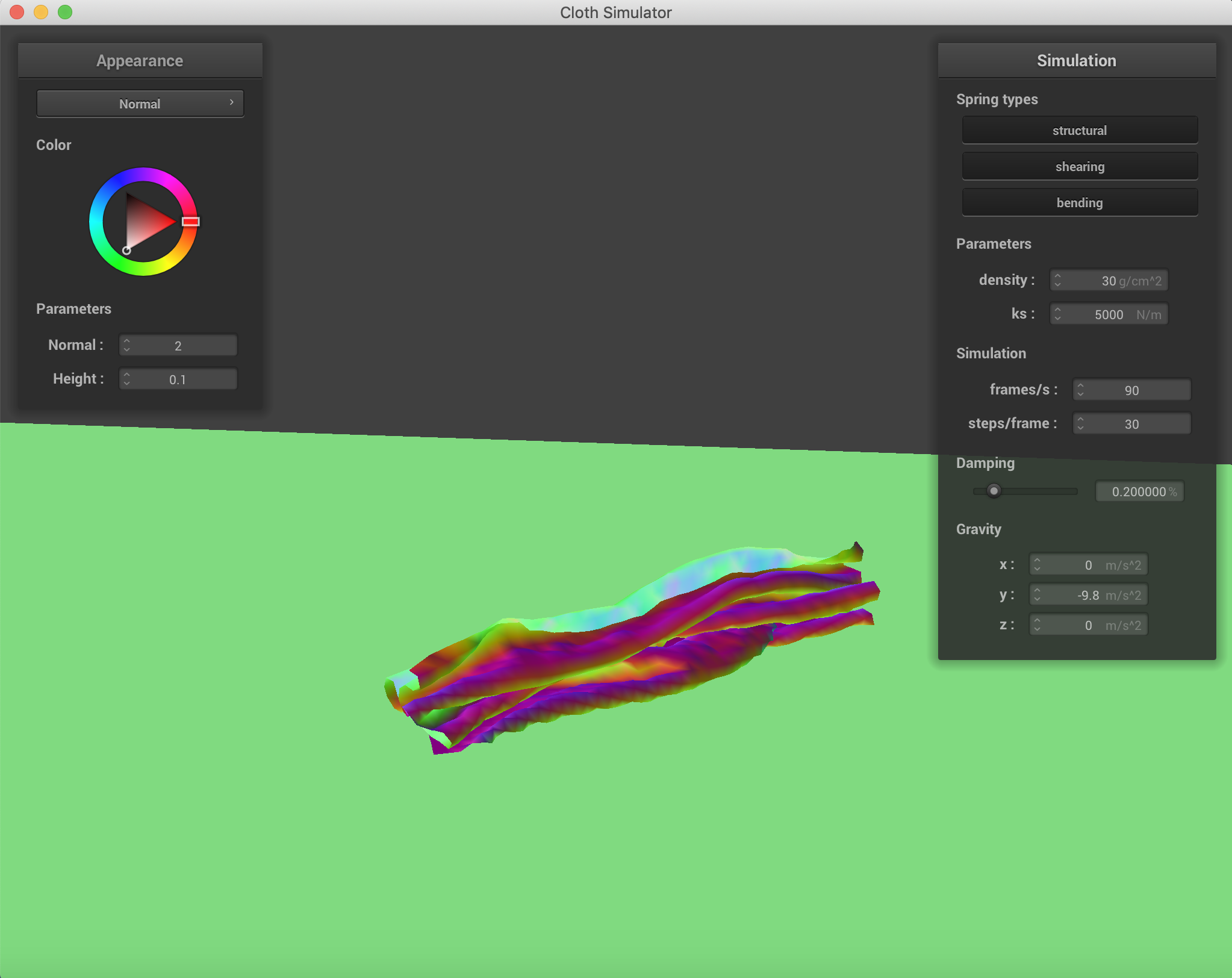
The falling cloth with varying forces in the x, y, and z directions. ks=5000 N/m.
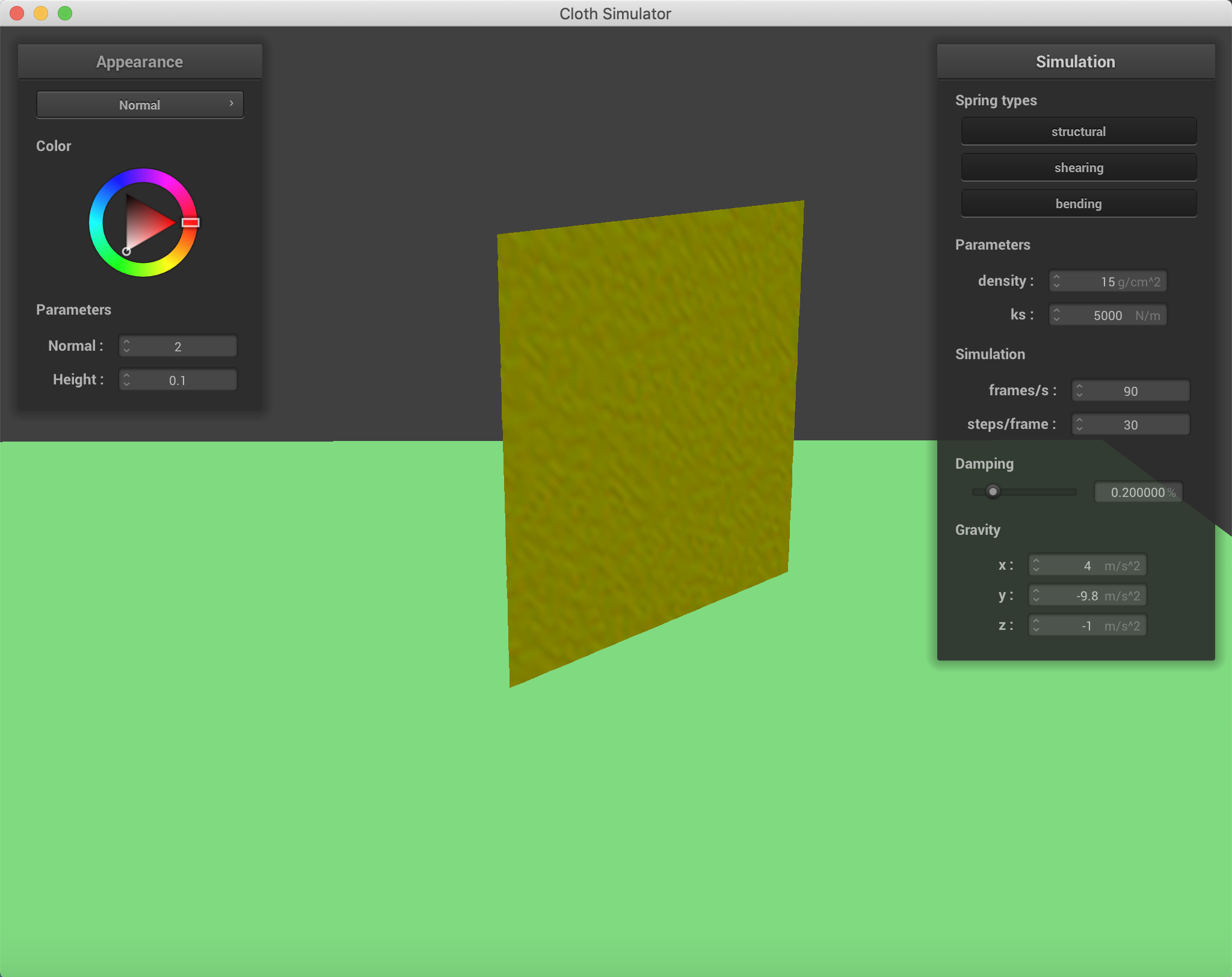
|
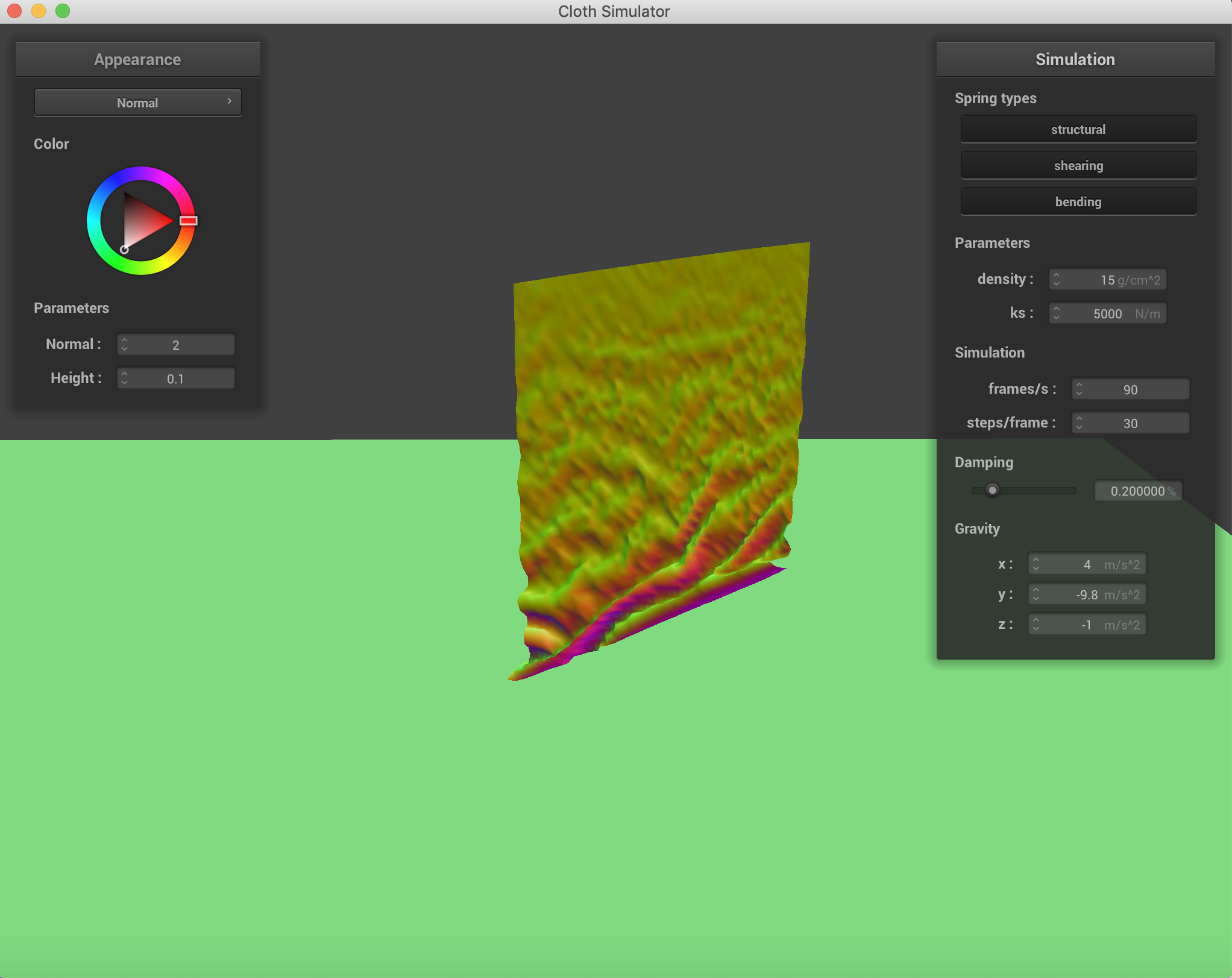
|
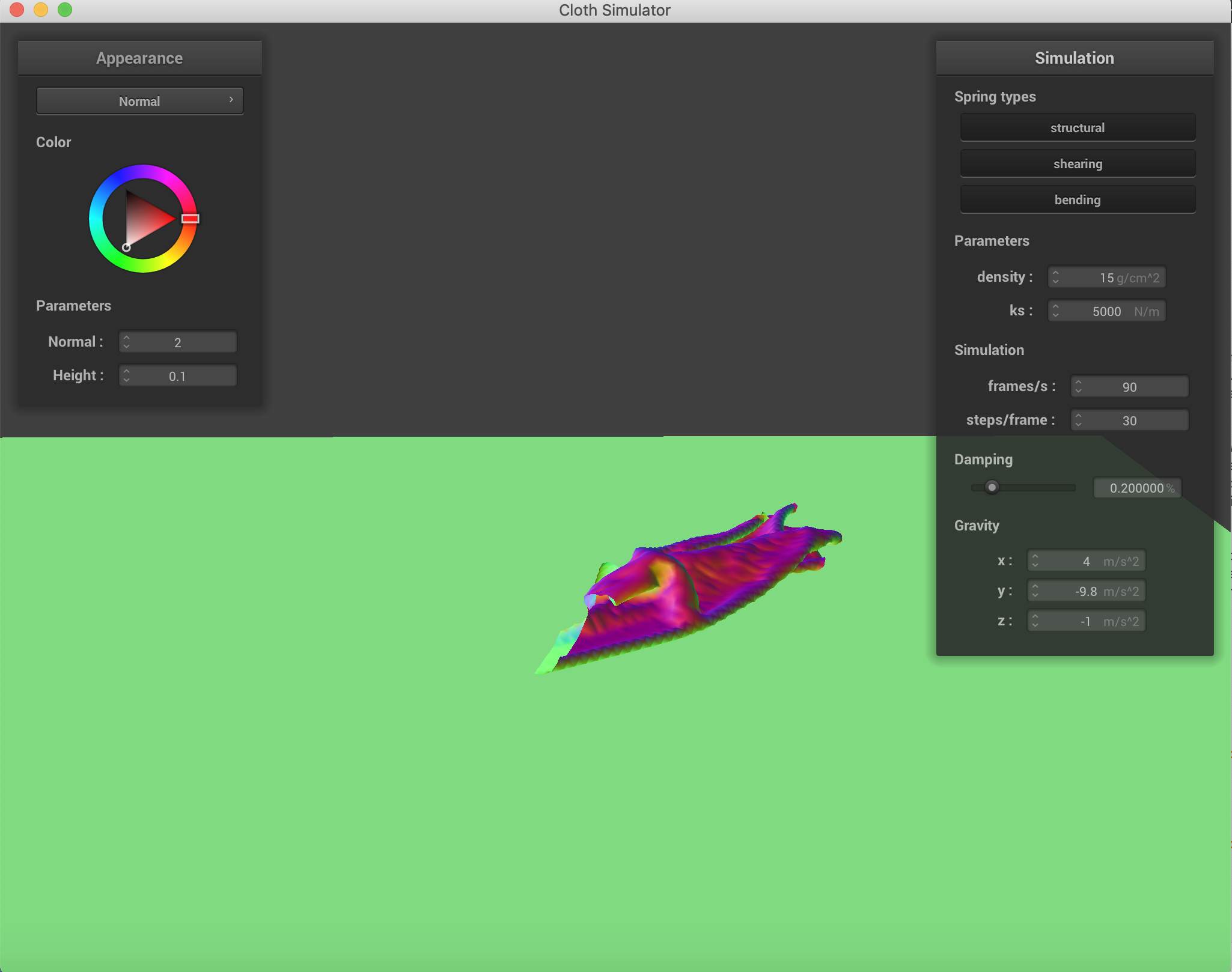
|
|
|
|
Some videos demonstrating the difference between self intersection and avoiding it.
|
When Self Intersections are not avoided. |
When Self Intersections are avoided. |
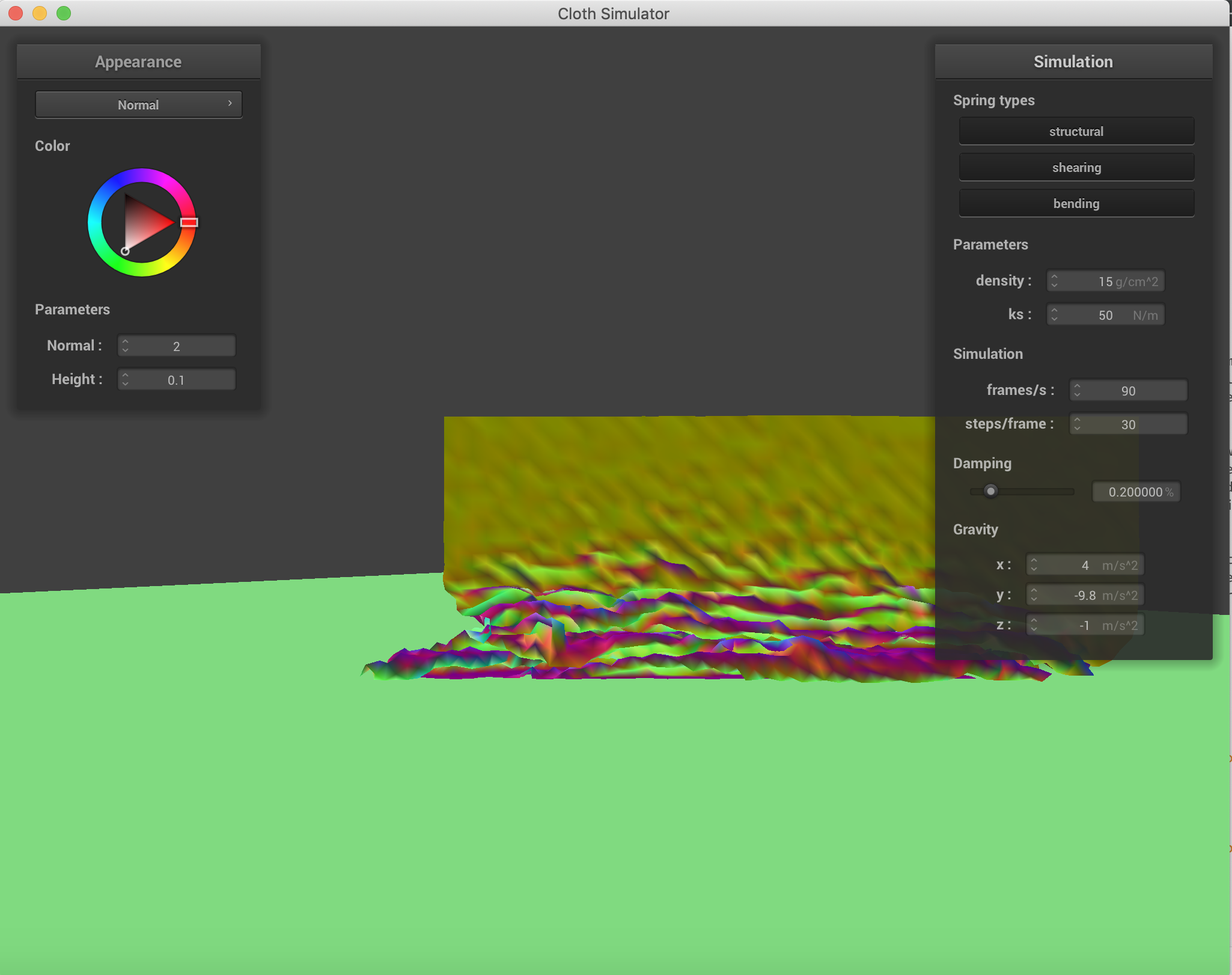
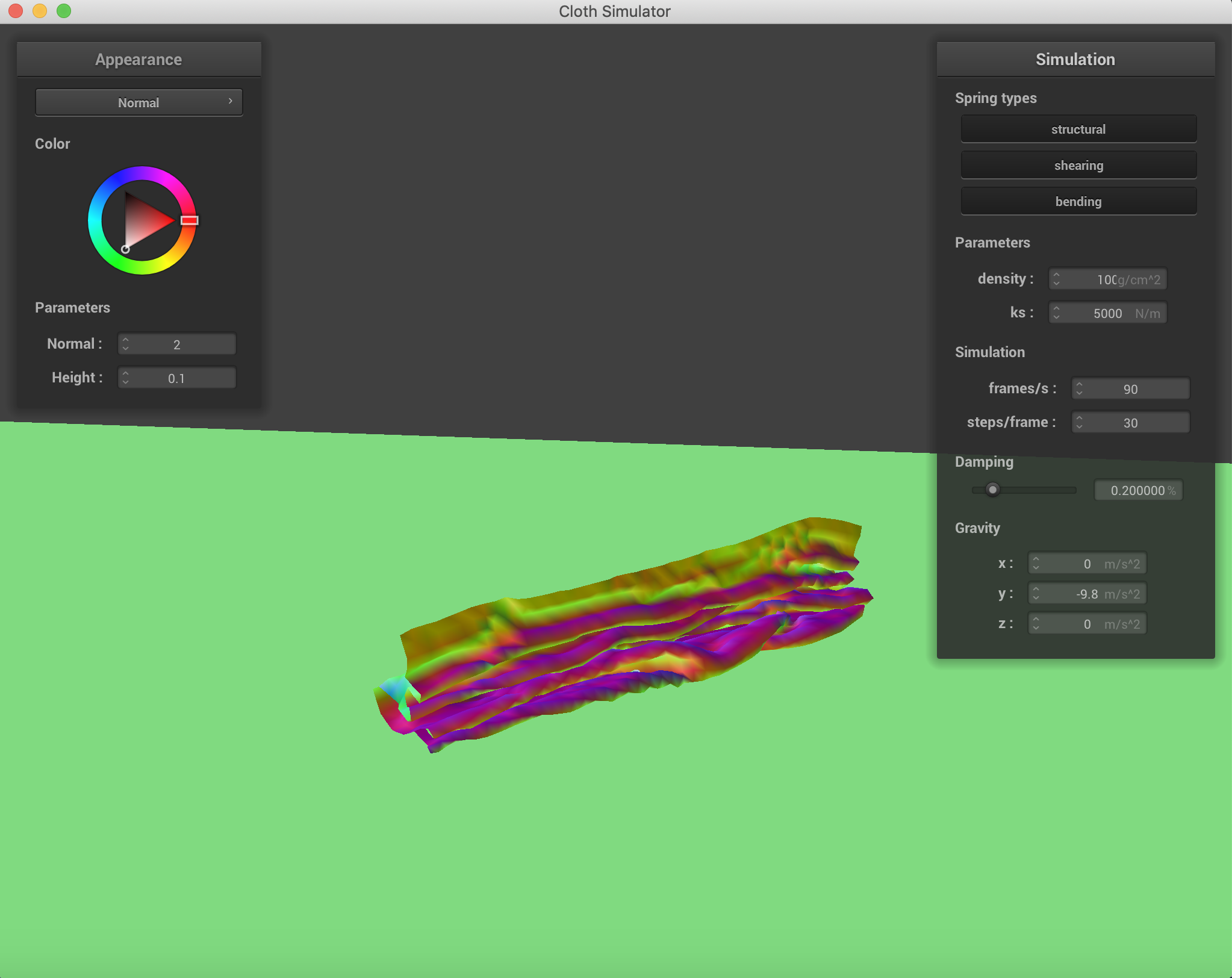
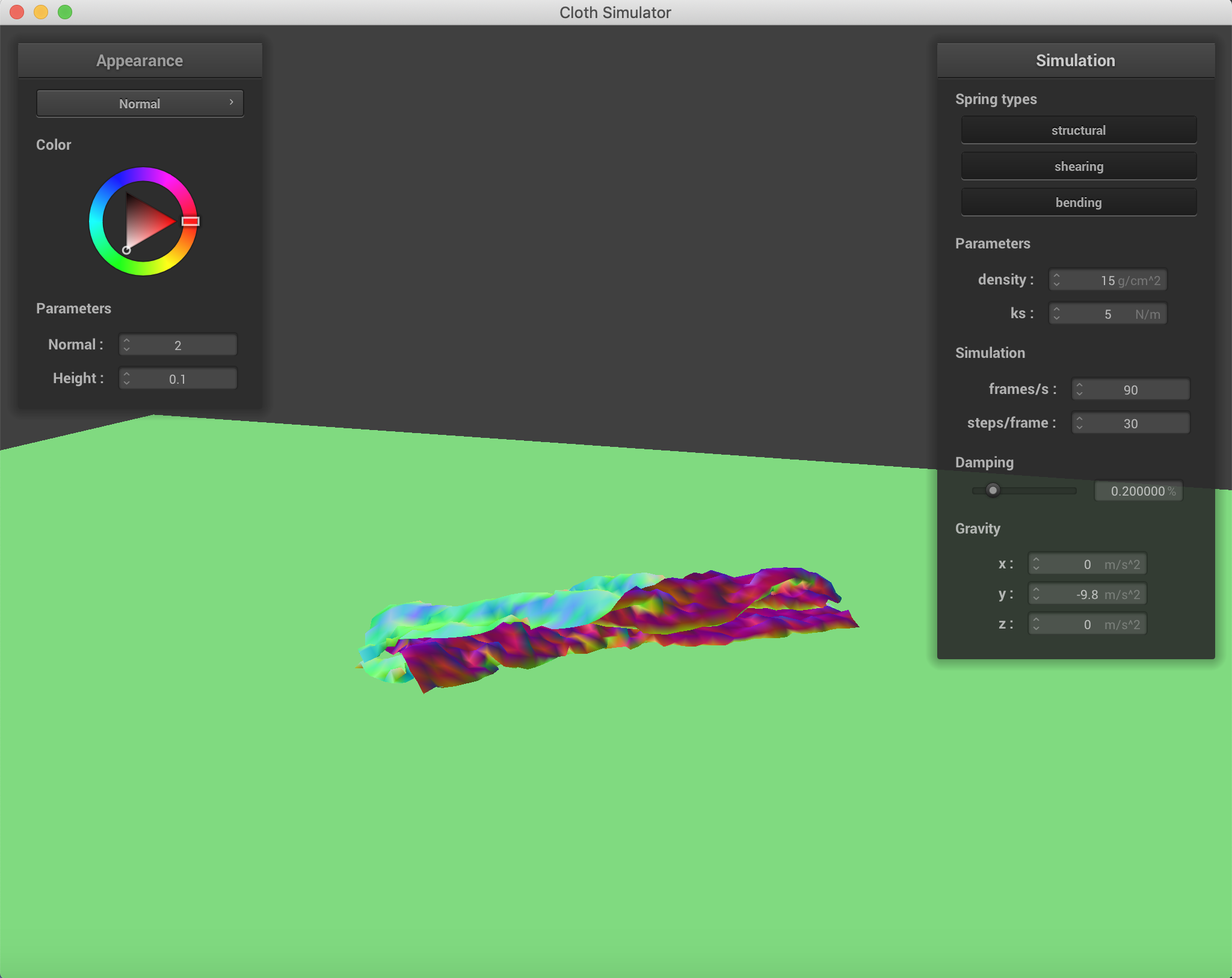
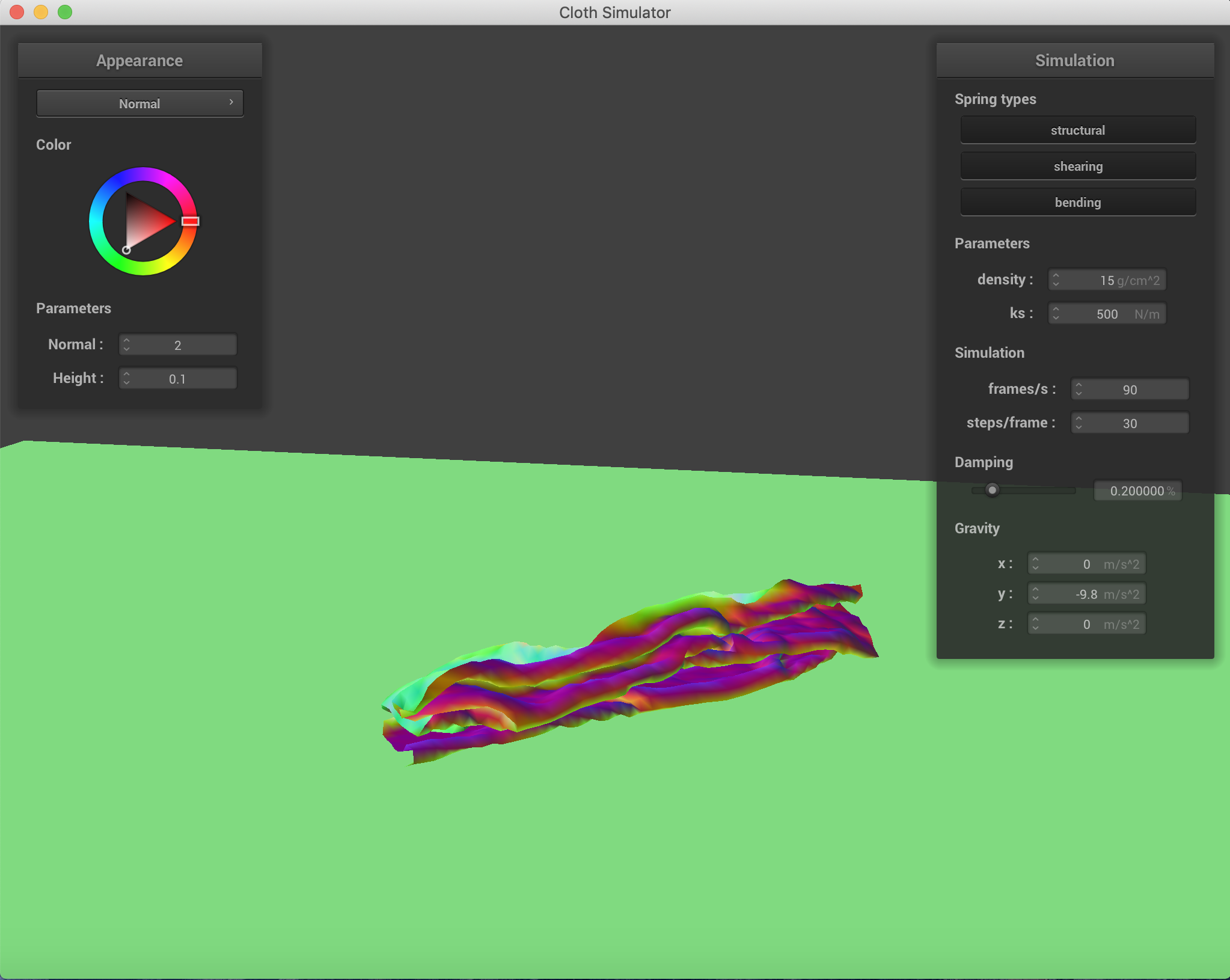
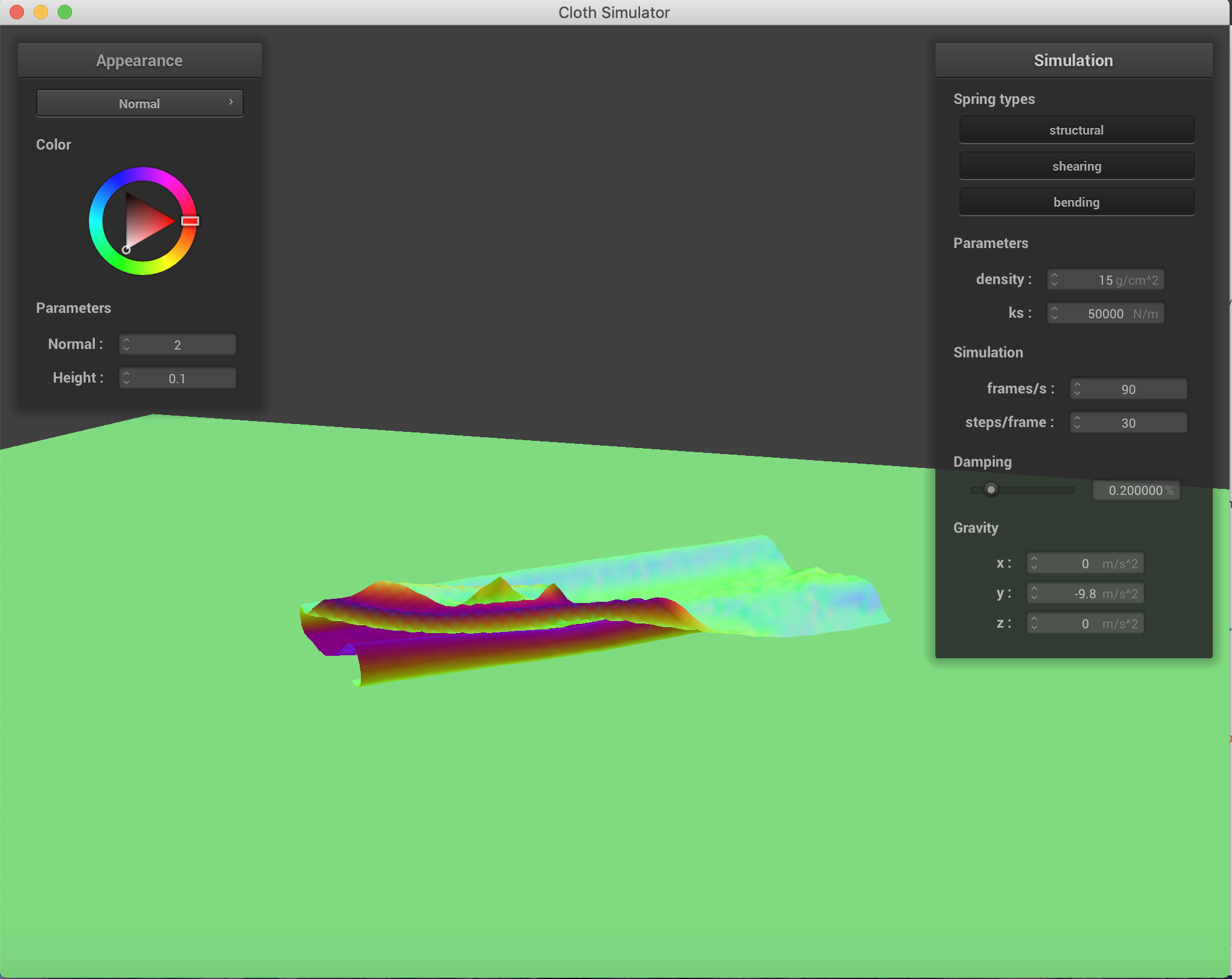
Varying the density and spirng constants to obtain different results in the falling. When the spring constant is lower, there are significantly more wrinkles and folds when the cloth falls. This is to be expected because force applied by the spring is a linear function of displacement and the spring constant, so the lower the constant, the lower the resistance force applied by the spring, and therefore the greater folding. When the density increases, the number of folds also increases, which is to be expected as a property of material density in nature when gravity is acting on it. All of these were conducted with only the force of gravity as an external force.
|
|
|
|
|
|

|
|
Part 5: GLSL Shaders
A shader is a mini program written in a language similar to C, which transforms inputs to outputs for different stages of the graphics pipeline. Most importantly, the shader calculates the rendering effects on a GPU rather than a CPU, enabling significant speedups and parallelization unavailable in ordinary CPU computing. A vertex shader applies transformatoins to vertices, modifying positions and normal vectors, and it writes varyings to send to the fragment shader. Fragment shaders process the fragments returned from rasterization. They take in the geometric attributes of the fragment that are computed by the vertex shaders, and then generate a color that is output for the rendering. An extreme simplification is that vertex shaders work on position and fragment shaders work on color.
The Blinn-Phong Model is calculated by the following equation.
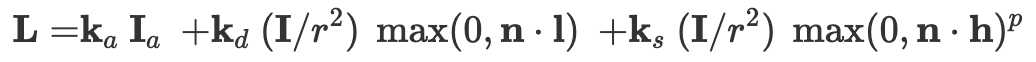
Blinn-Phong is a modification to the Phong shading model in which the shader must continually recalculate the dot product of the vector towards the viewer and the vector towards the light source. Blinn's modification uses the calculation of a half vector, the bisector of the light source and viewer vectors. The dot product of the surface normal and the bisector vector represents the half of the cosine of the angle originally represented by the dot product of the light and viewer vector. Blinn-Phong is more efficient for infinite point light sources. The Blinn-Phong formula we use accumulates the light components from ambient light, specular light, and diffuse light.
The four component variations of the Blinn-Phong Model
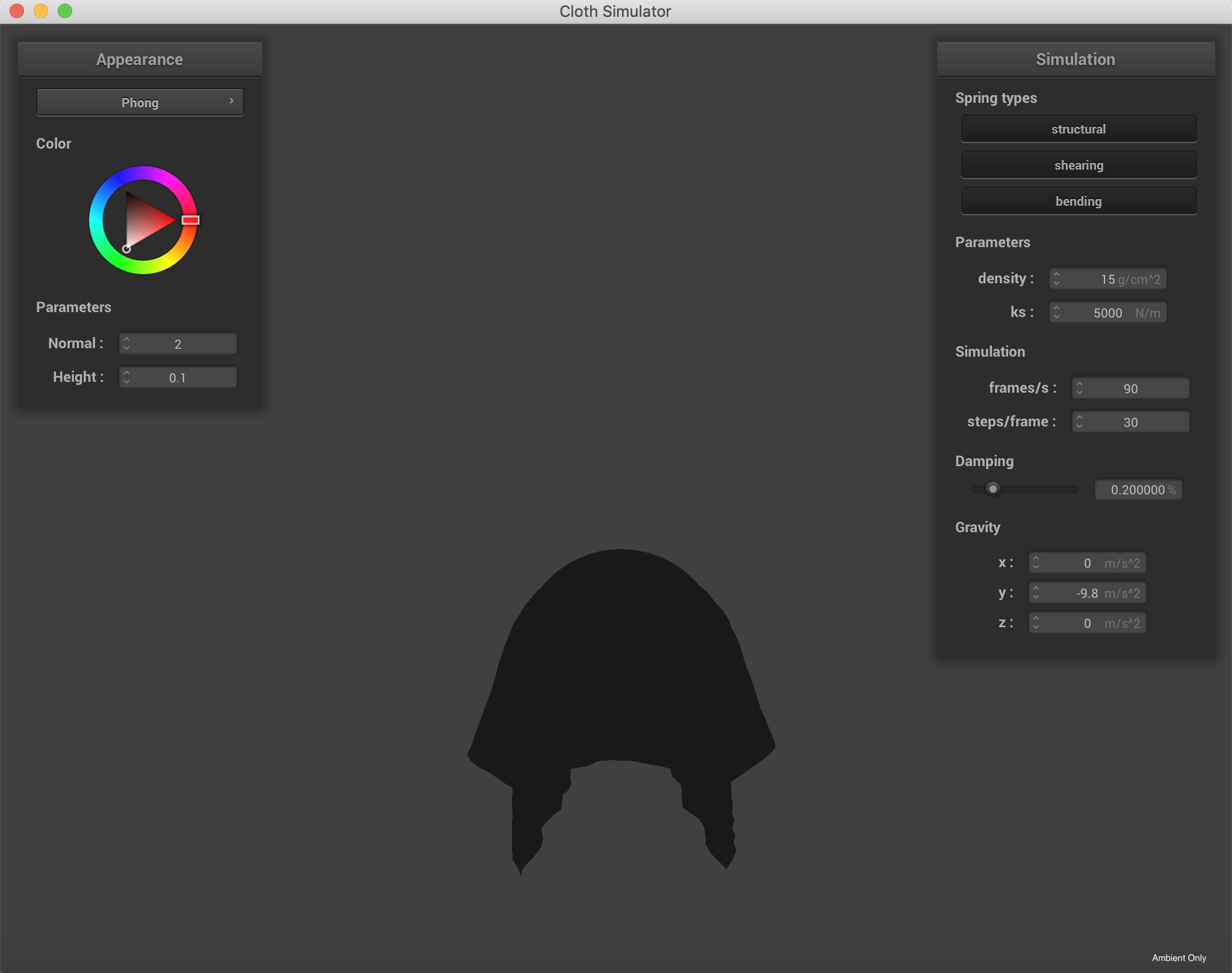
|
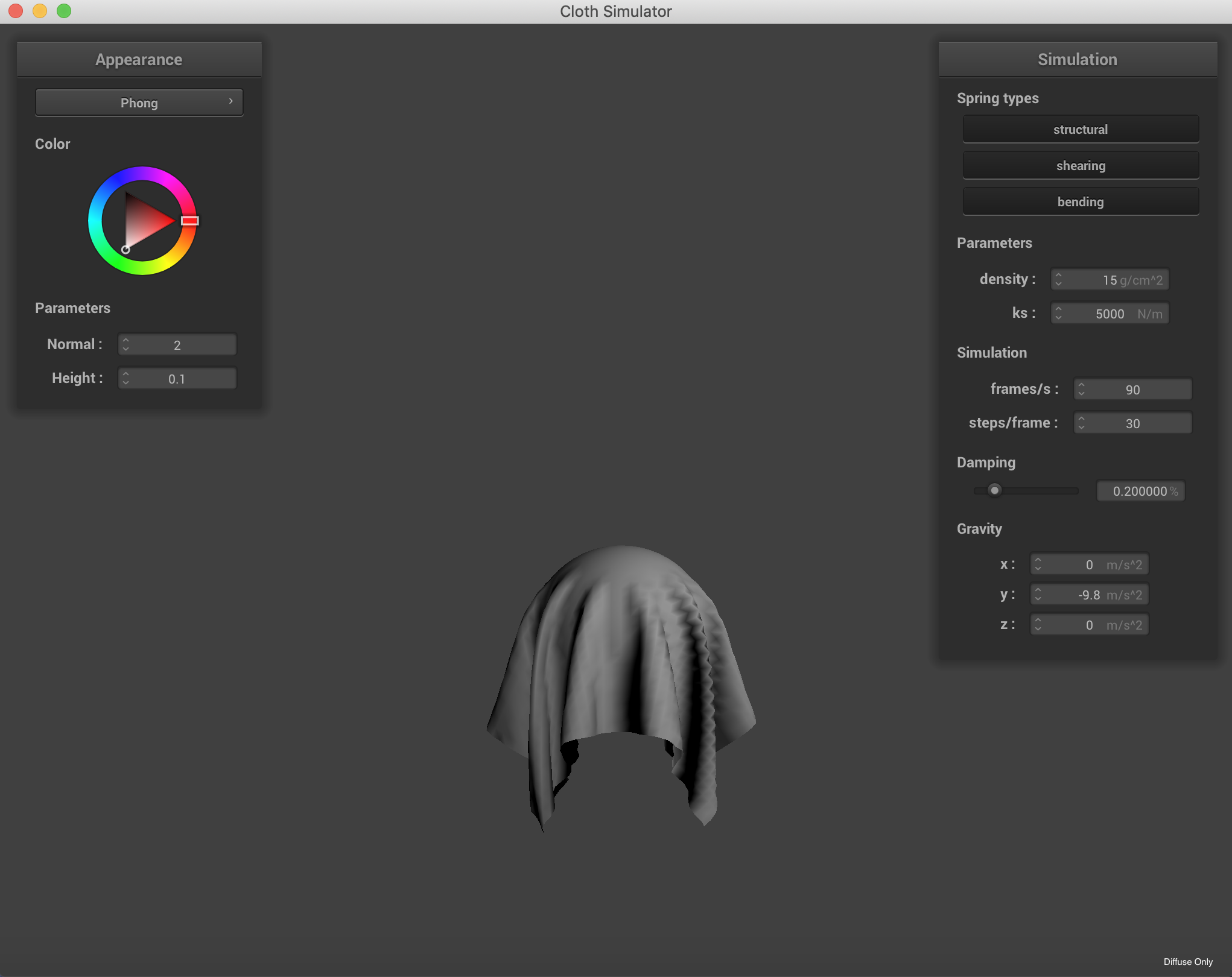
|
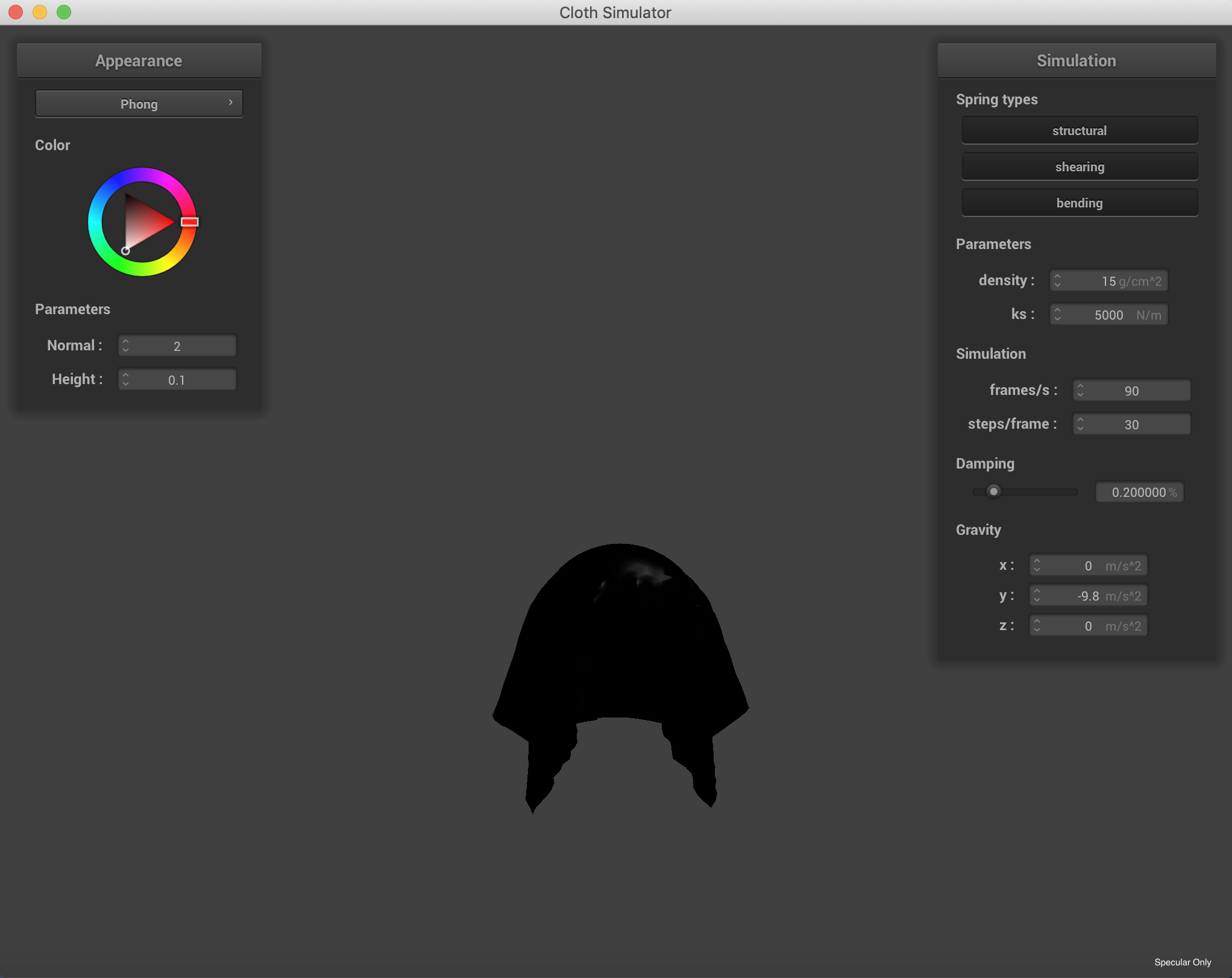
|
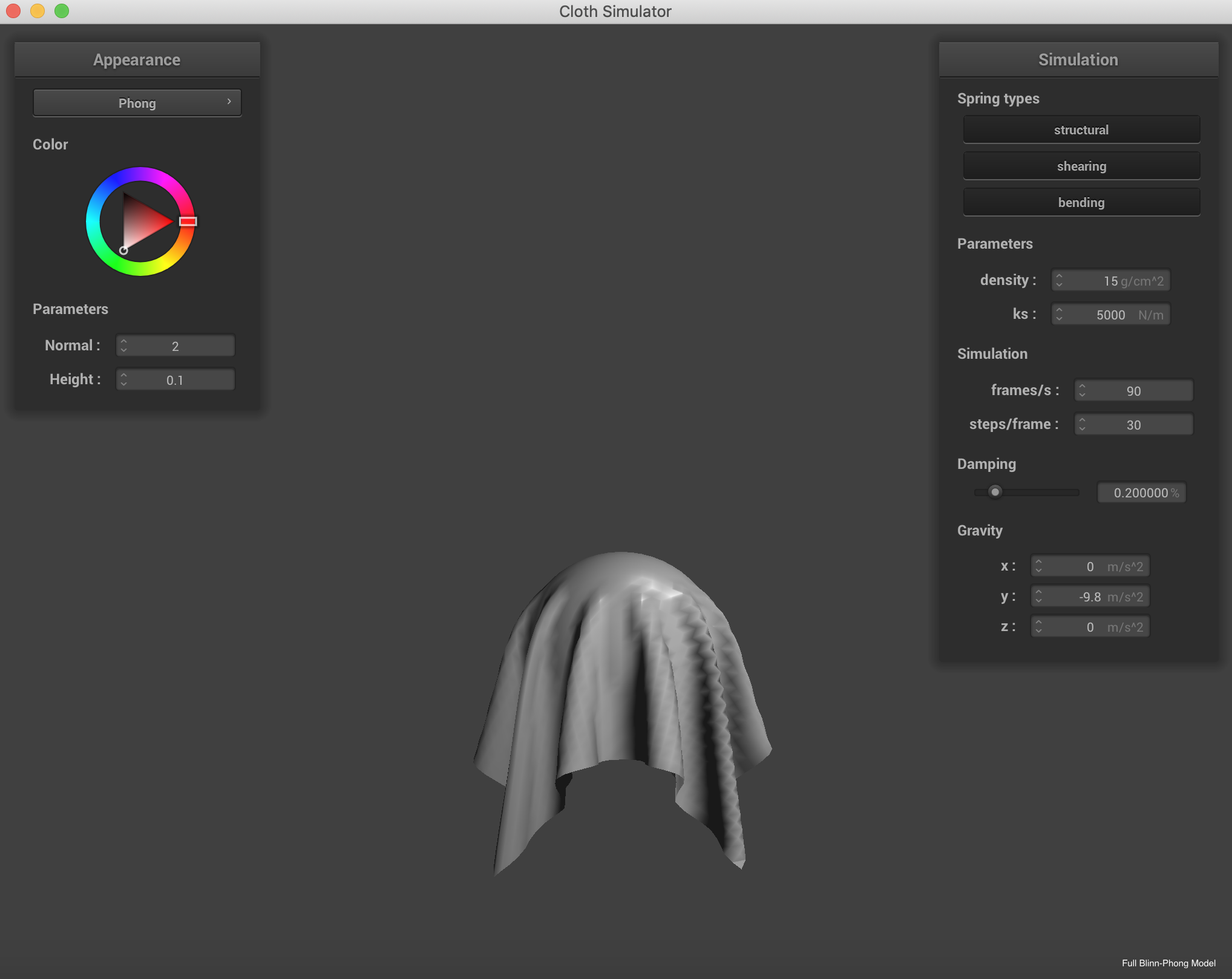
|
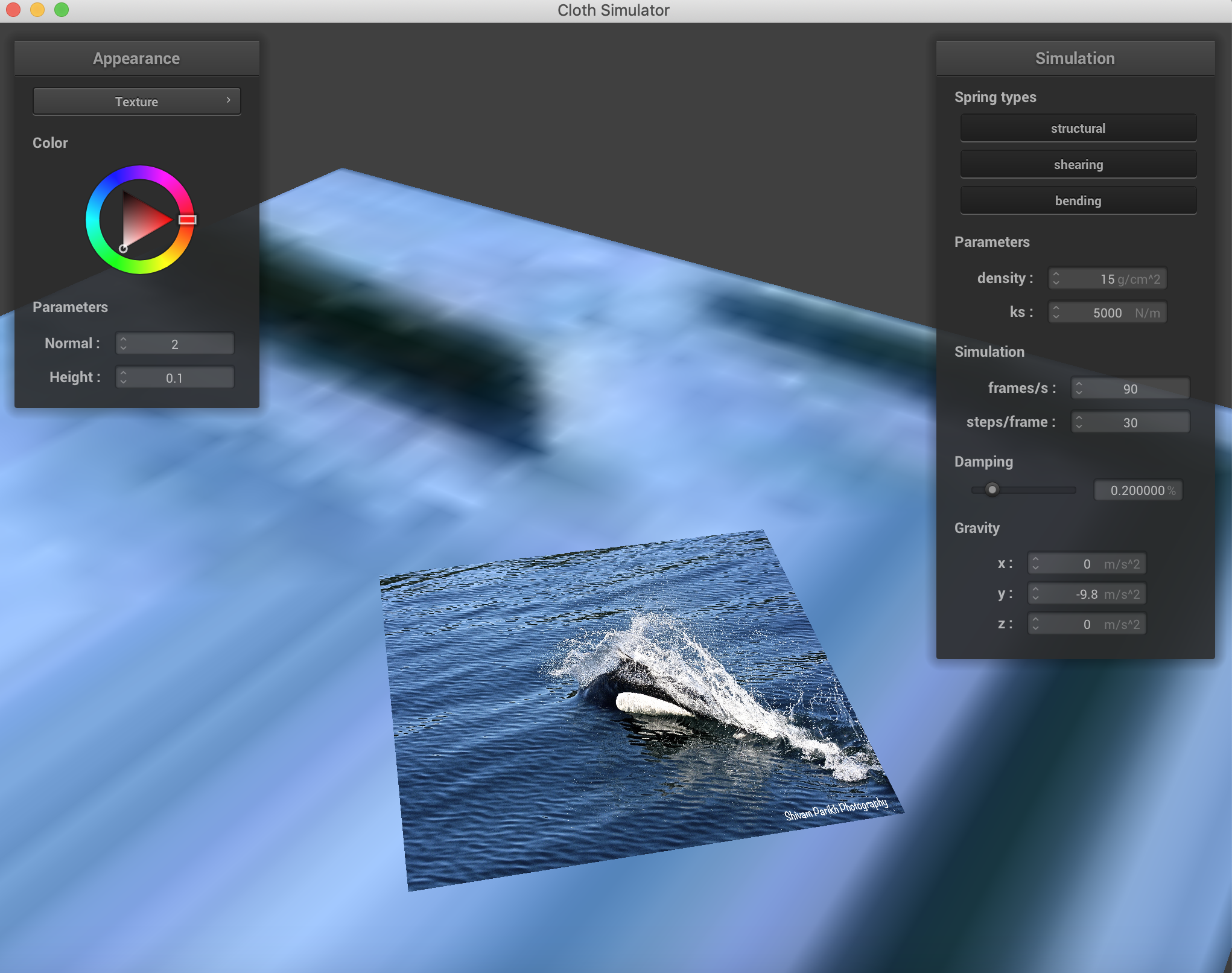
Displaying the use of custom textures. This is a photo of a Dall's Porpoise I took in the Alaskan Fjords.
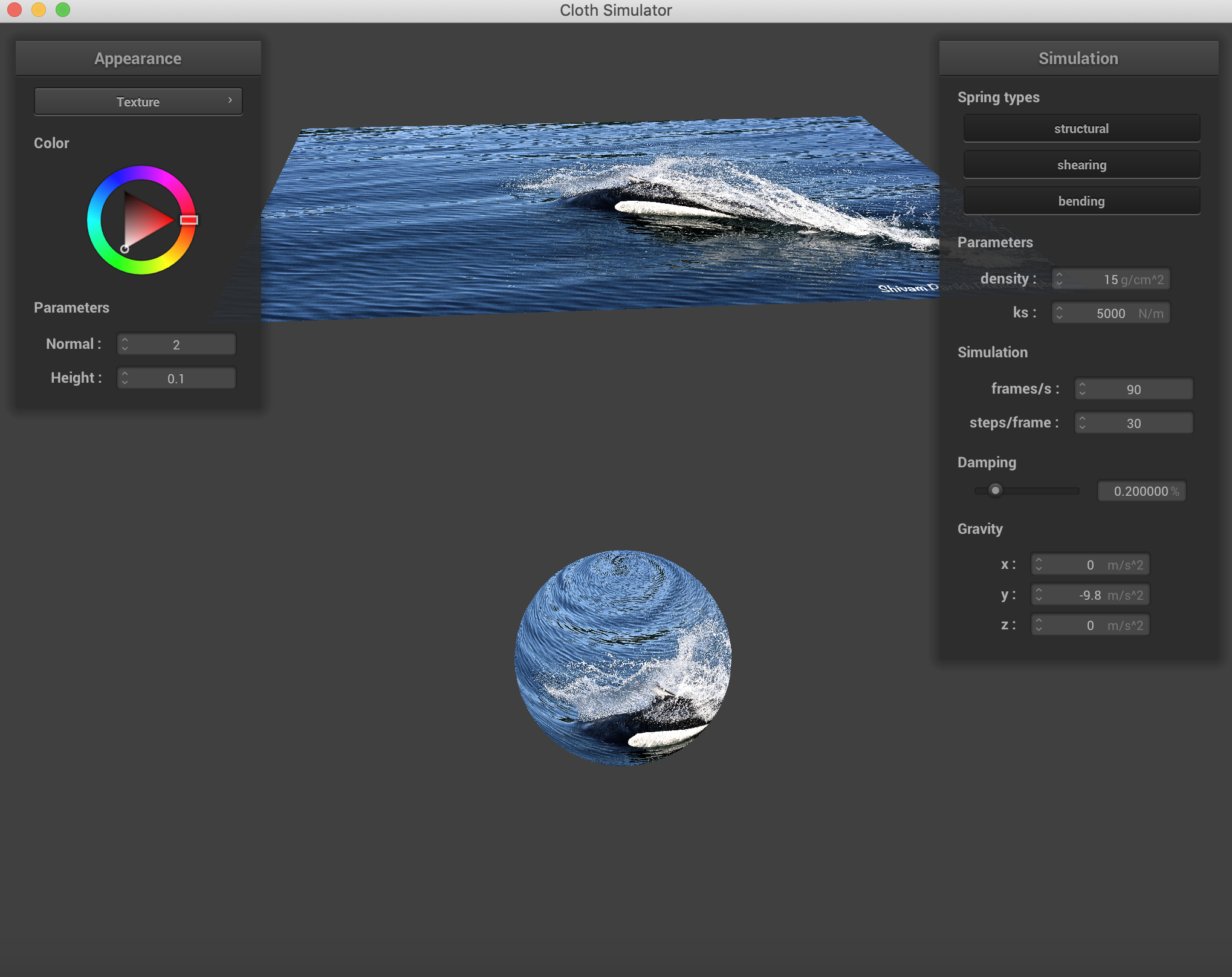
|
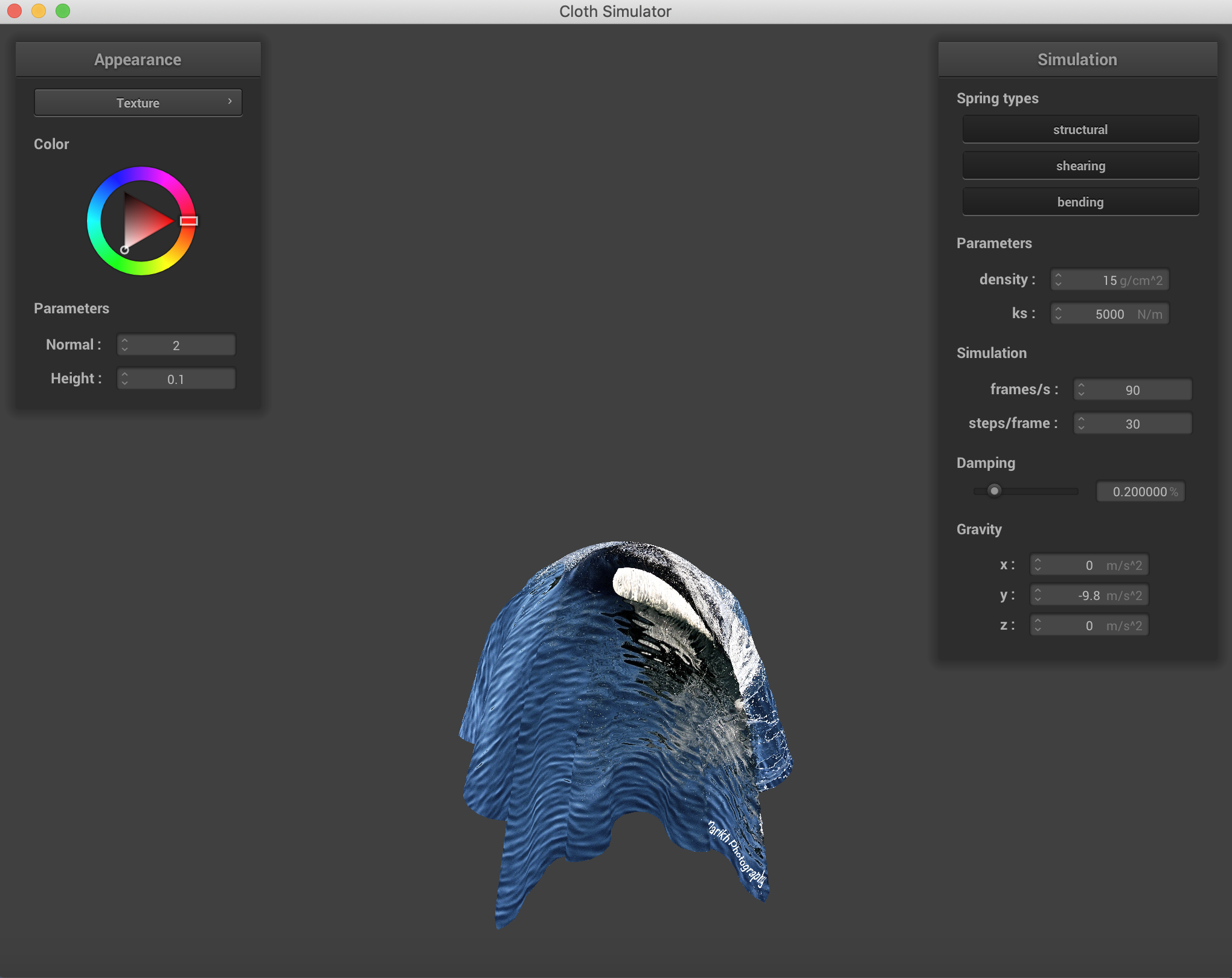
|
Below is the demonstration of Bump Mapping and Displacement Mapping. The bump mapping doesn't show much of a change with the added coarseness, but the displacement mapping has some mild, though mostly invisible benefits. The main one is that the gap in the lower coarseness image disappears in the higher coarseness image.
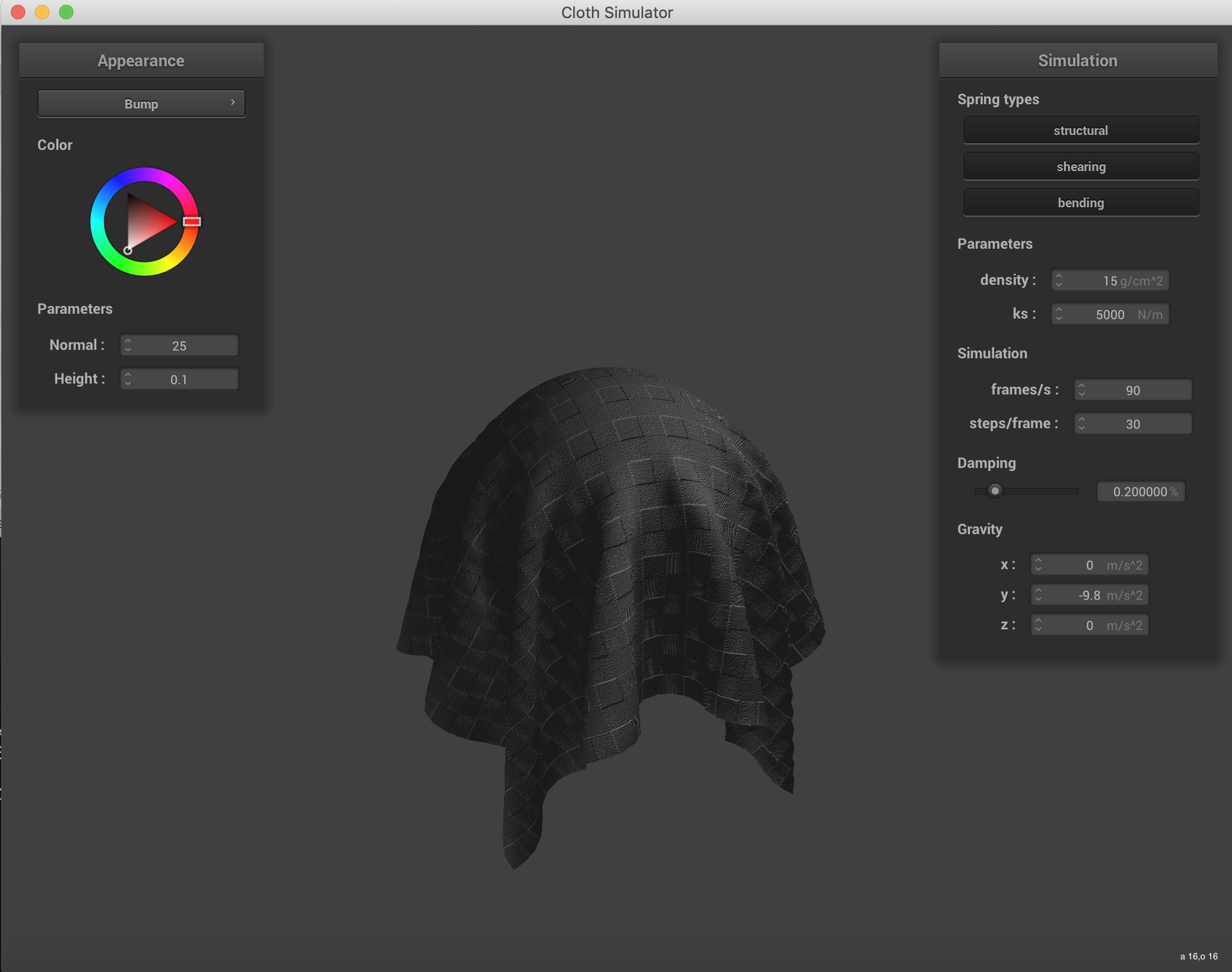
|
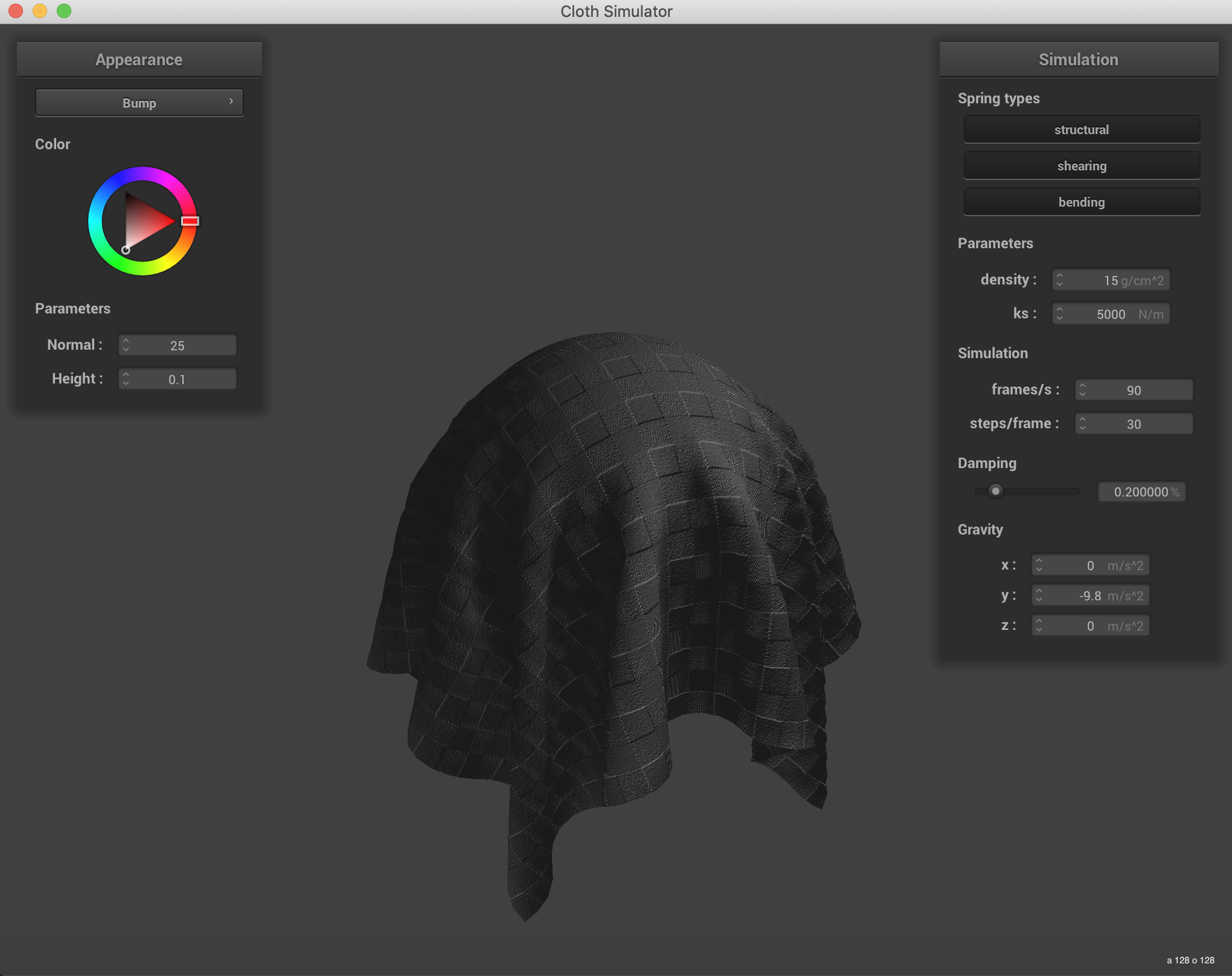
|
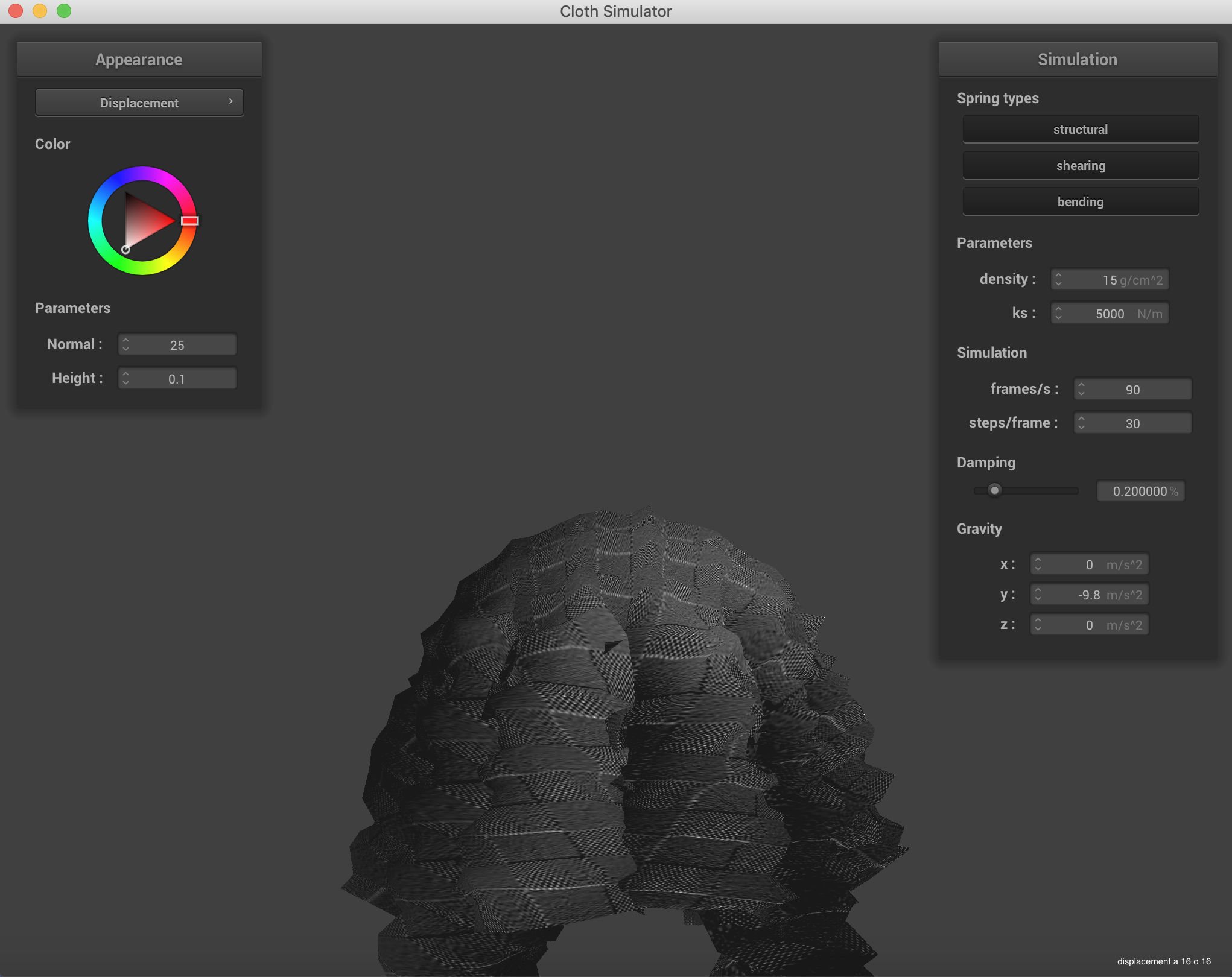
|
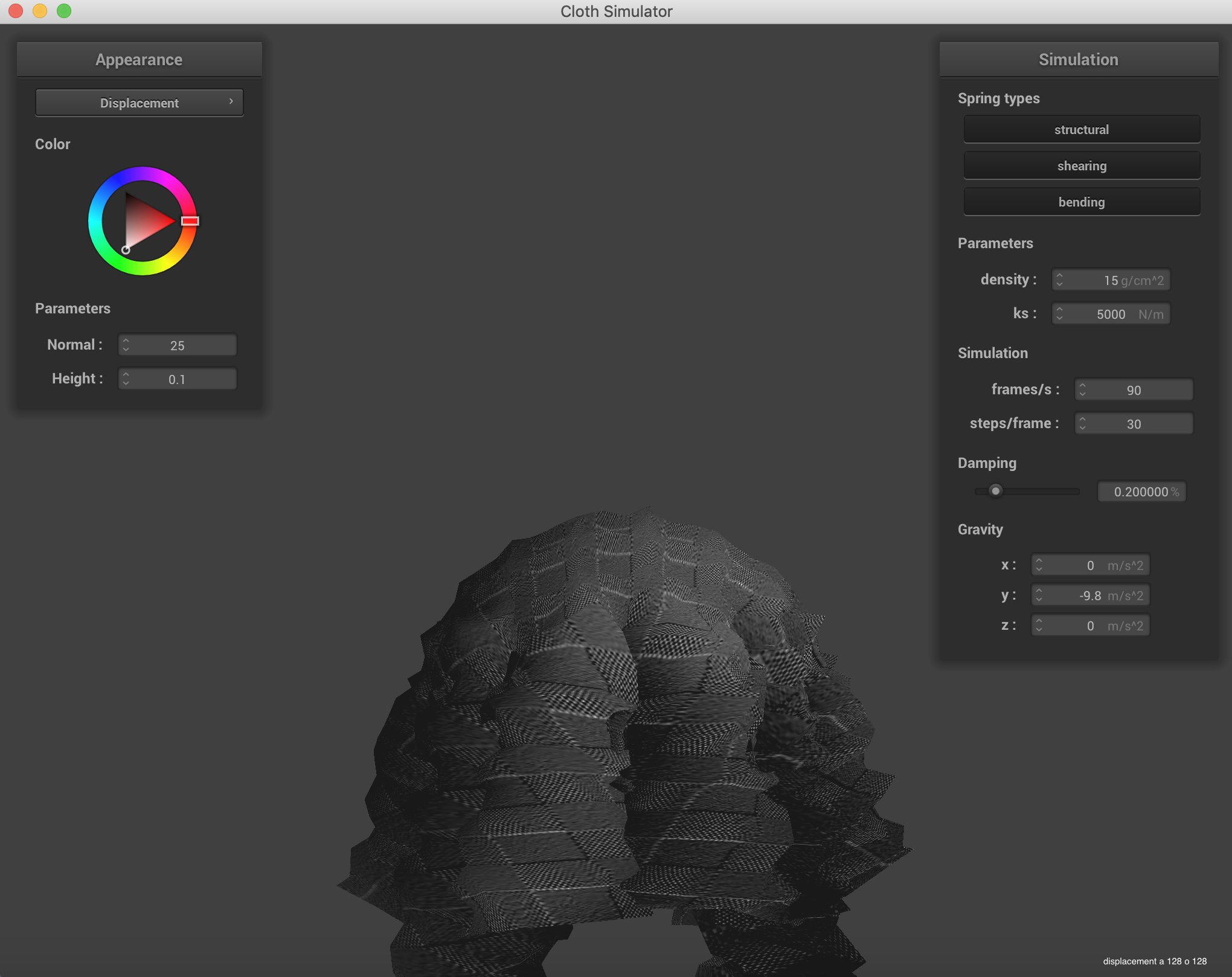
|
Here are a few of the mirror examples I made, both on the pinned surfaces and the sphere.
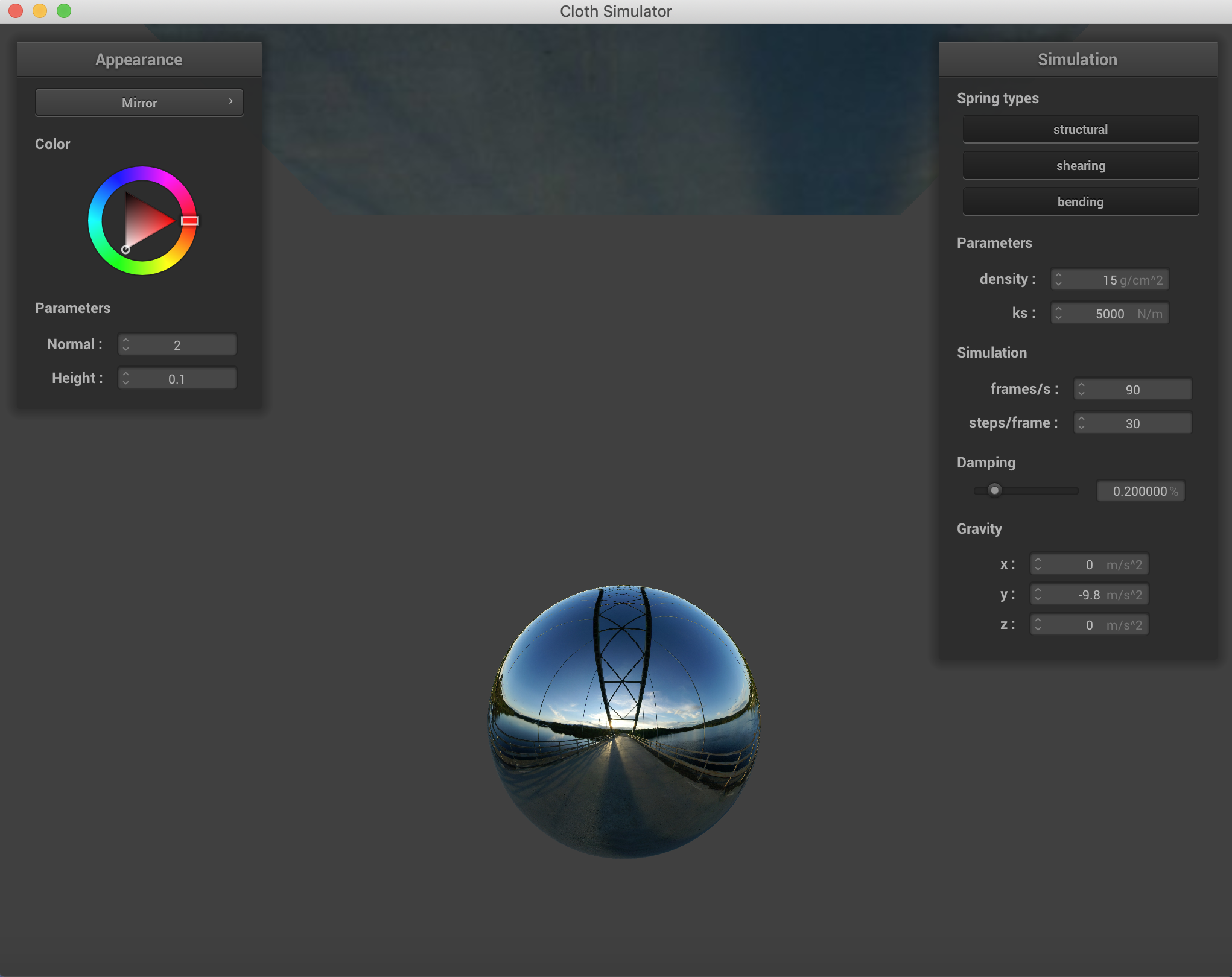
|
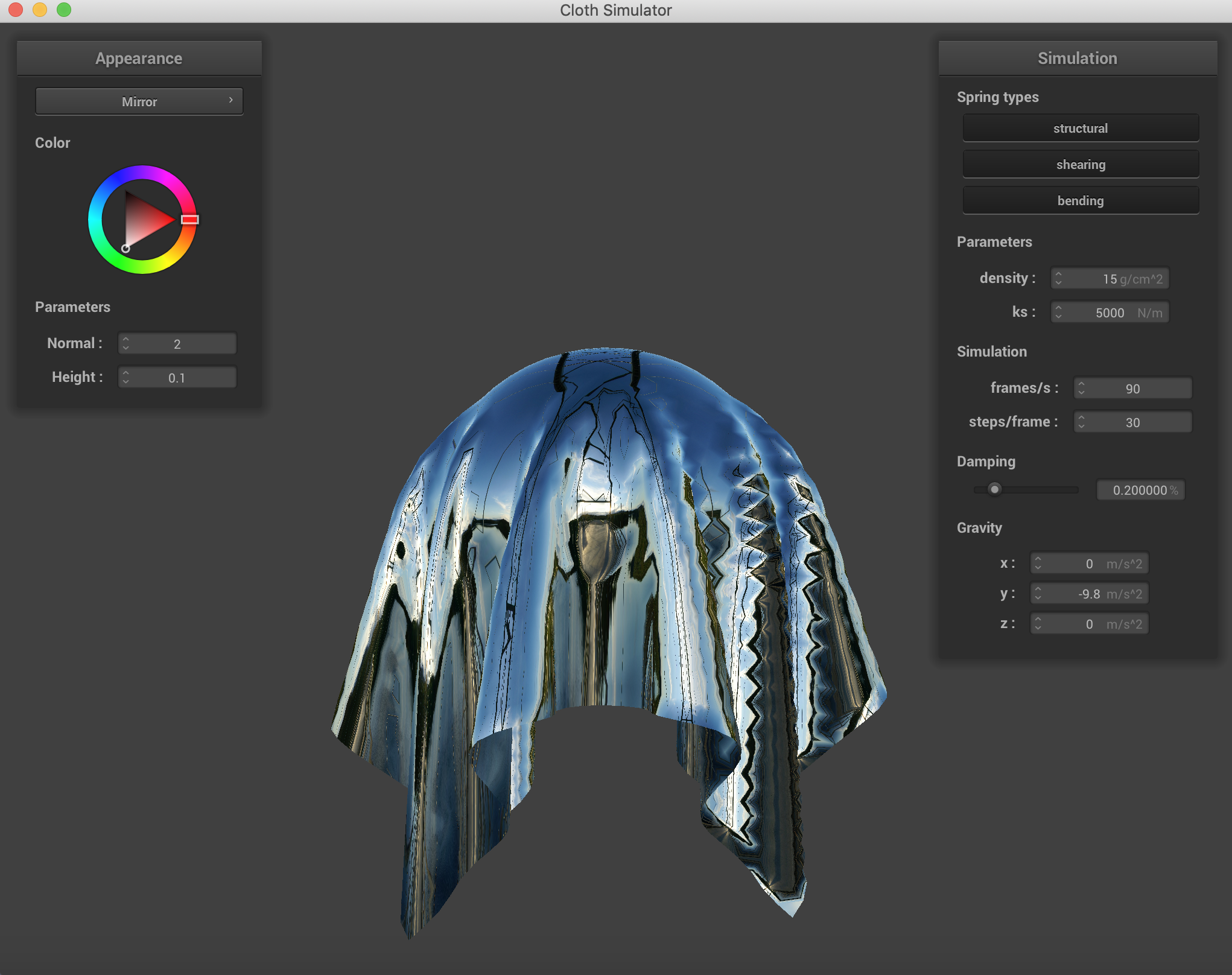
|
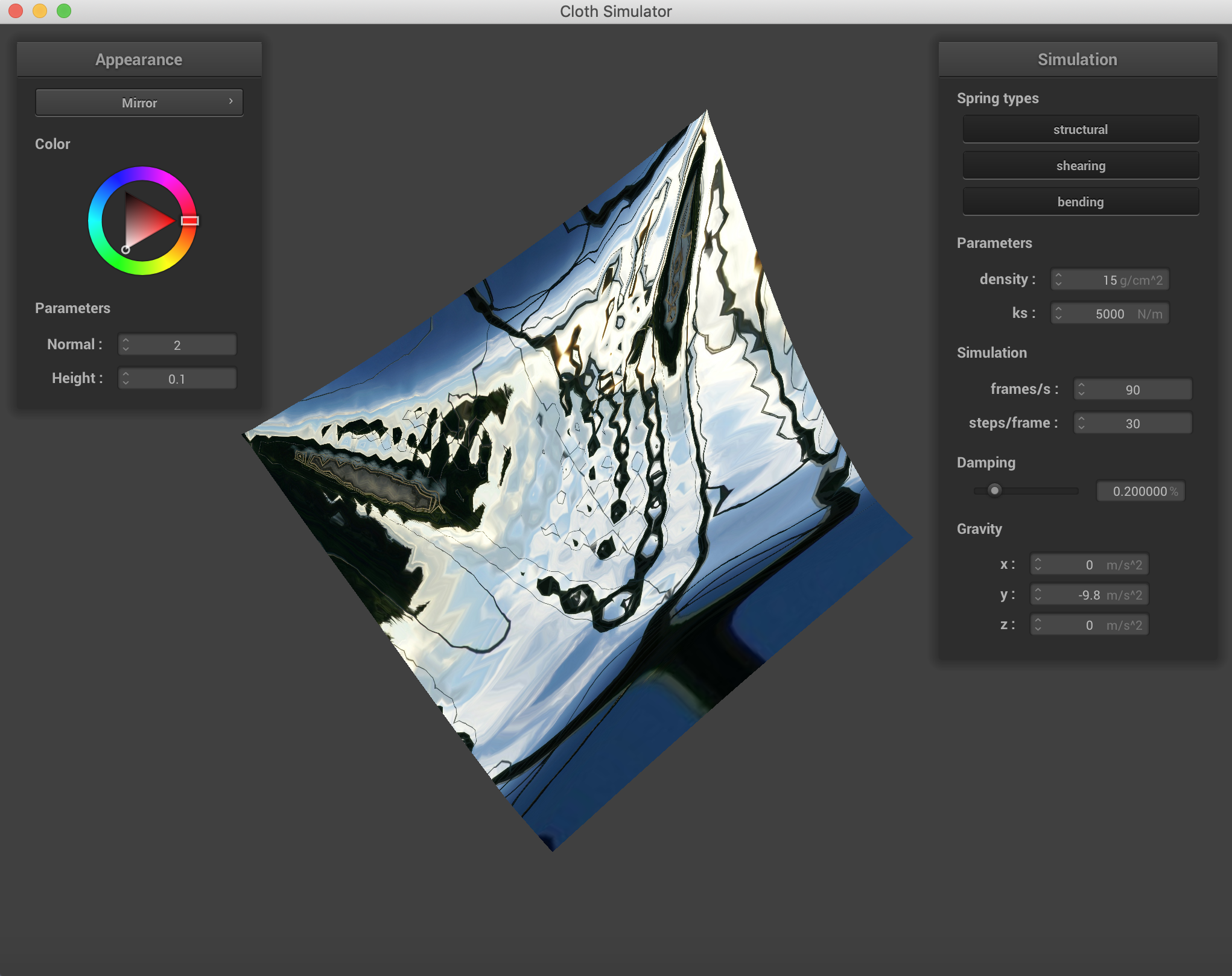
|
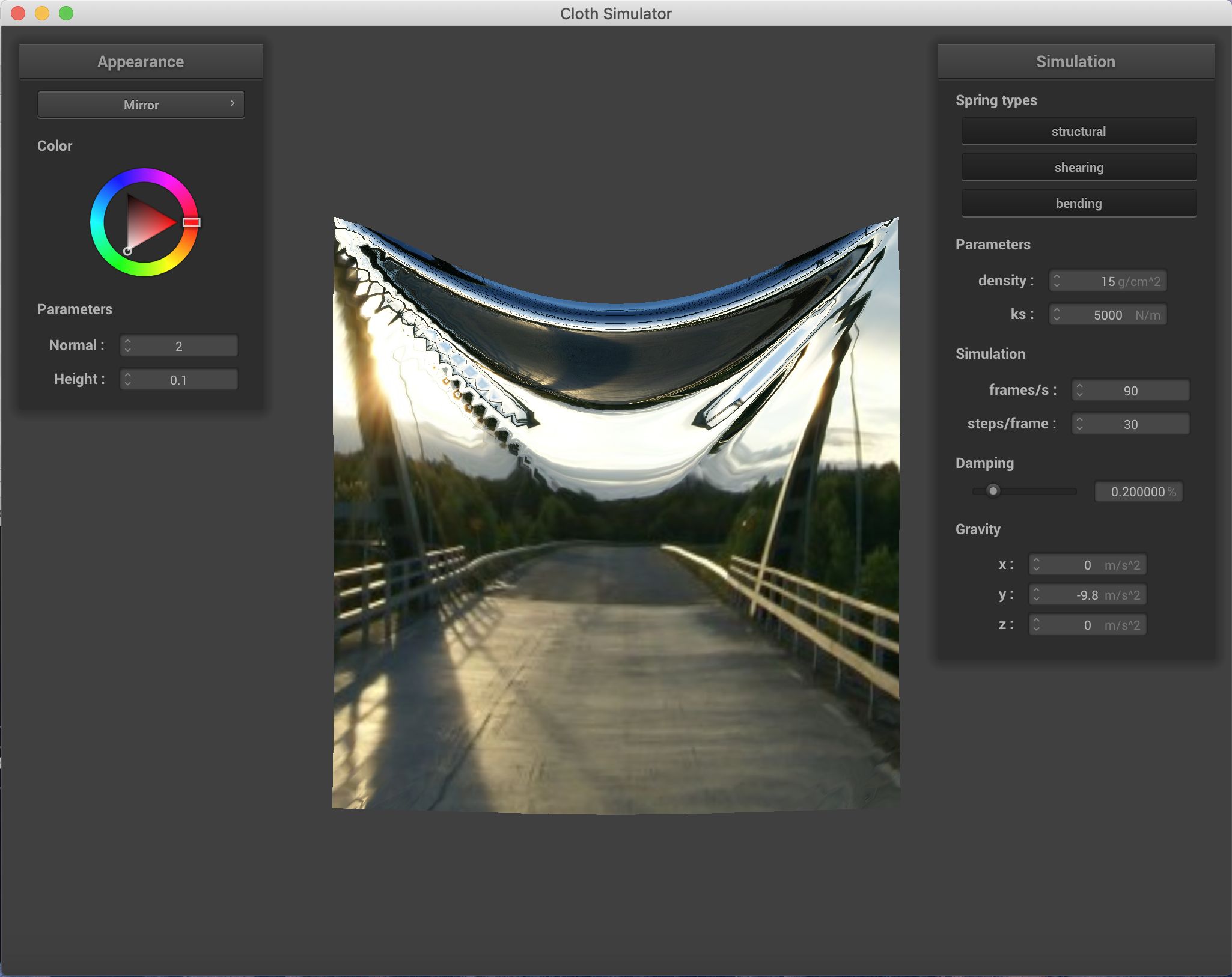
|