Overview
In this project, we built an implementation of a Rasterer. The final product was a vector graphics renderer that could render SVGs as PNGs. What I thought was neat about this project was how it used classes and inheritance to enable us to work with different layers of the rasterization pipeline. For example, drawing lines and points was already enabled, but we started by rendering triangles, and then worked on coloring triangles, and then worked on applying textures to triangles.
Section I: Rasterization
Part 1: Rasterizing single-color triangles
In Part 1, we learn to rasterize single color triangles. While this originally seemed pretty simple based on the line test we learned in class, it turns out the ordering of the points (clockwise or counter-clockwise) played an important role in the coloring of our images. This part began with assigning colors to the singe sub-pixel sample in fill_color. The Color class stored RGB in floats between [0, 1], so before assigning color values as unsigned chars, I converted the floats to whole numbers in the range [0, 256).
The second task was to fill in a basic implementation of DrawRend::rasterize_triangle. This involved the triangle line test from lecture.
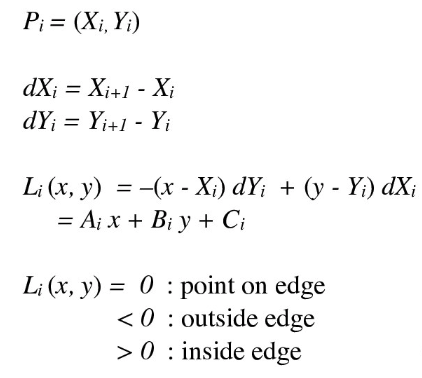
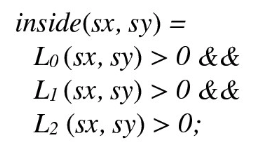
Rather than check all the points in the frame to see if they are in/out of the triangle, we create a bounding box for the points of the triangle. The bounding box is created using the max and min x and y coordinates of the triangle. By only iterating through the points in the bounding box, my algorithm is no worse than simply checking each sample within the bounding box. To make sure we check each sample only once, I compute the line equations at the beginning, and compute the in/on/out of each point simultaneously. To deal with clockwise and counterclockwise ordering of triangle vertices, I have a check at the beginning to determine the direction of points. If the direction was clockwise, then I multiplied the line equations by a negative 1 multiplier to ensure that the equations were testing for points inside the triangle defined by the given ordering of points. If the direction was counterclockwise, the line equations stayed the same, so the only check was a multiplicative function and it only had to be computed once per call to DrawRend::rasterize_triangle, so it was also efficient.
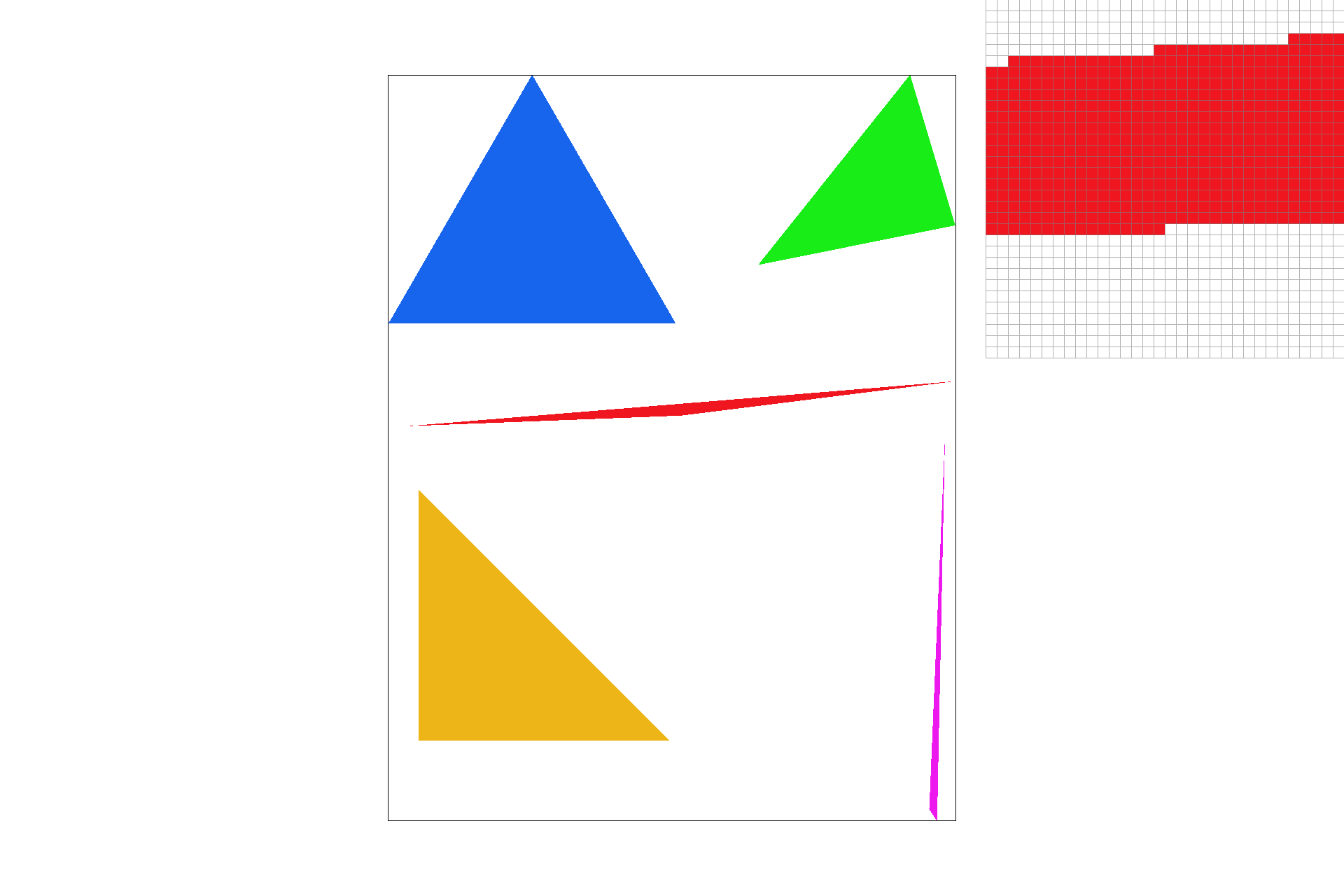
Part 2: Antialiasing triangles
I implemented supersampling by adding another pair of for loops over the domain of the new sub-resolution within the original pixel domain. This size was decided by the square root of the scale resolution. Supersampling is useful because during the line test, we may identify some points near edges of lines or at narrow intersection points as being not in the shape, but in fact they might just not be discretely in the shape. So to make sure they are mimicking the ability to be in the shape, we do some color shading and get smoother images as shown below. Pay attention to the zoomed locations at the tip of the pink triangle for a visible change in smoothness.
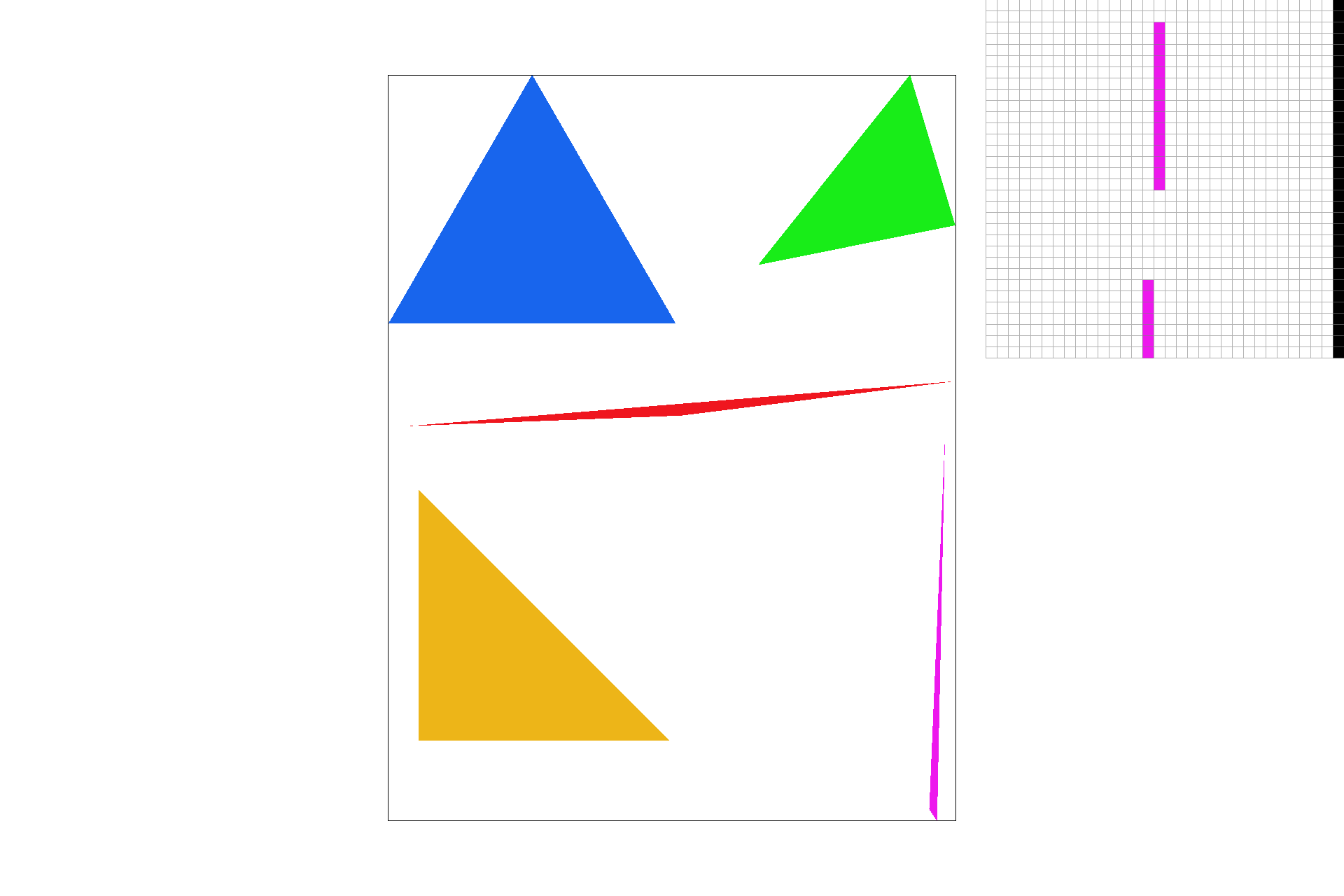
|
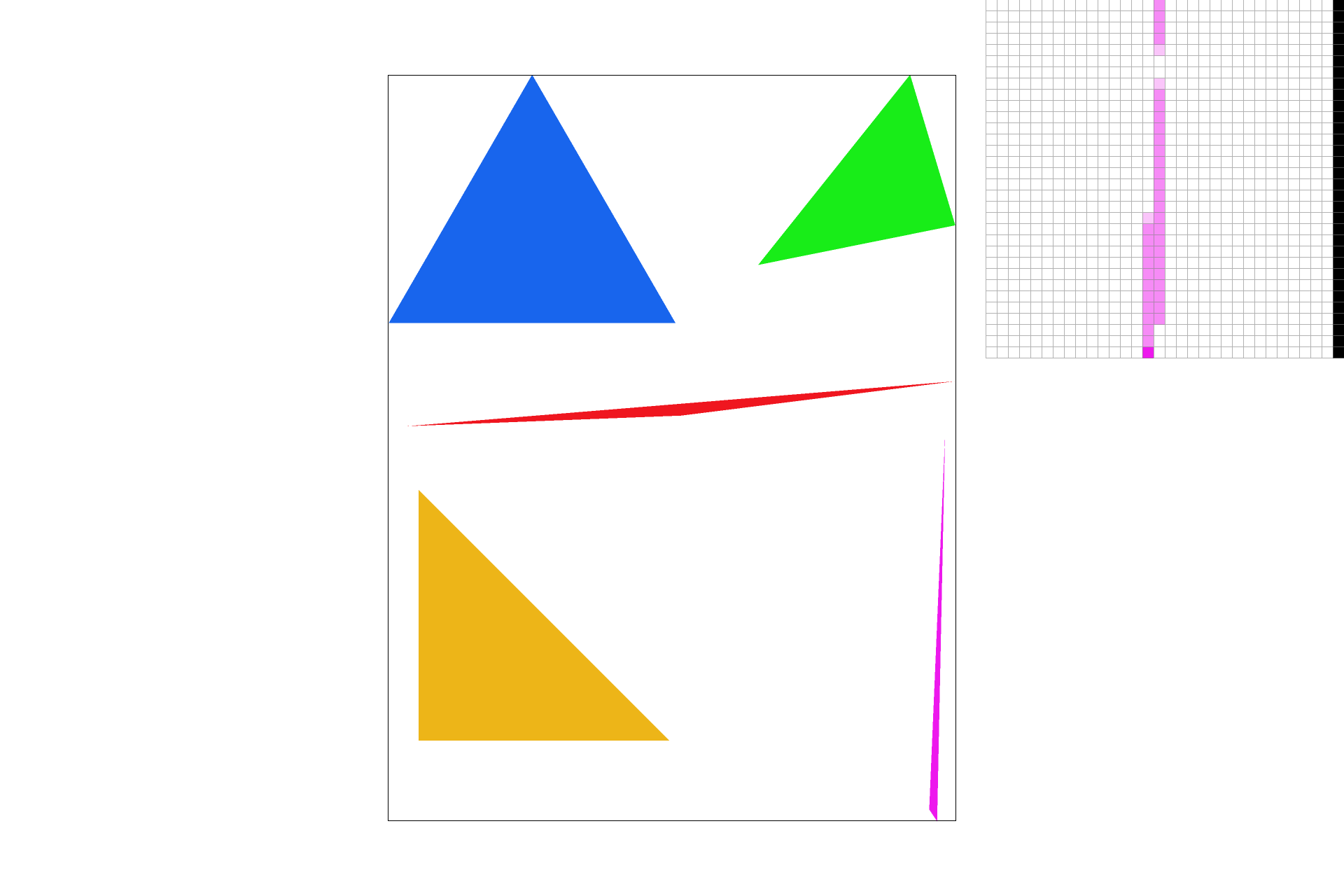
|
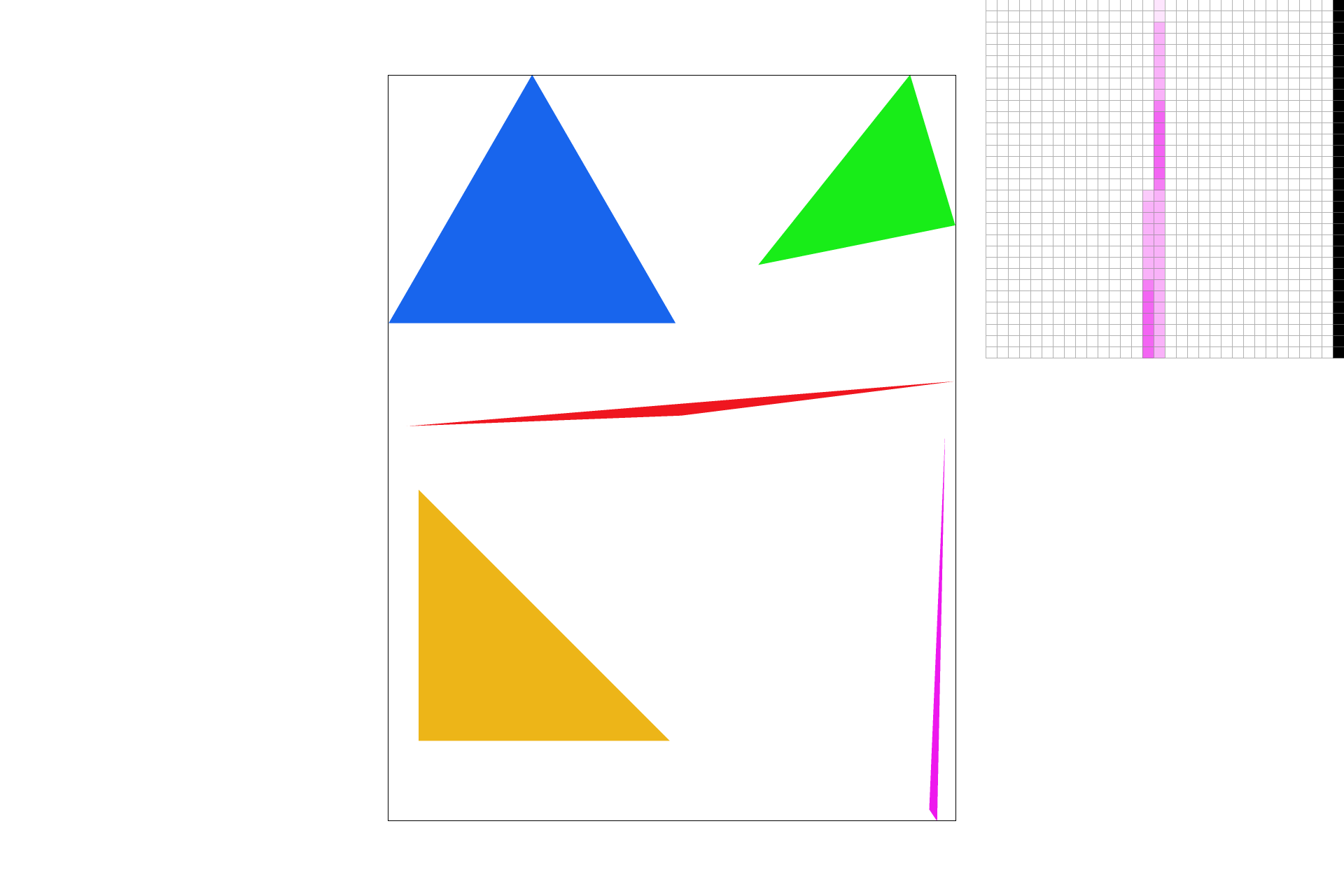
|
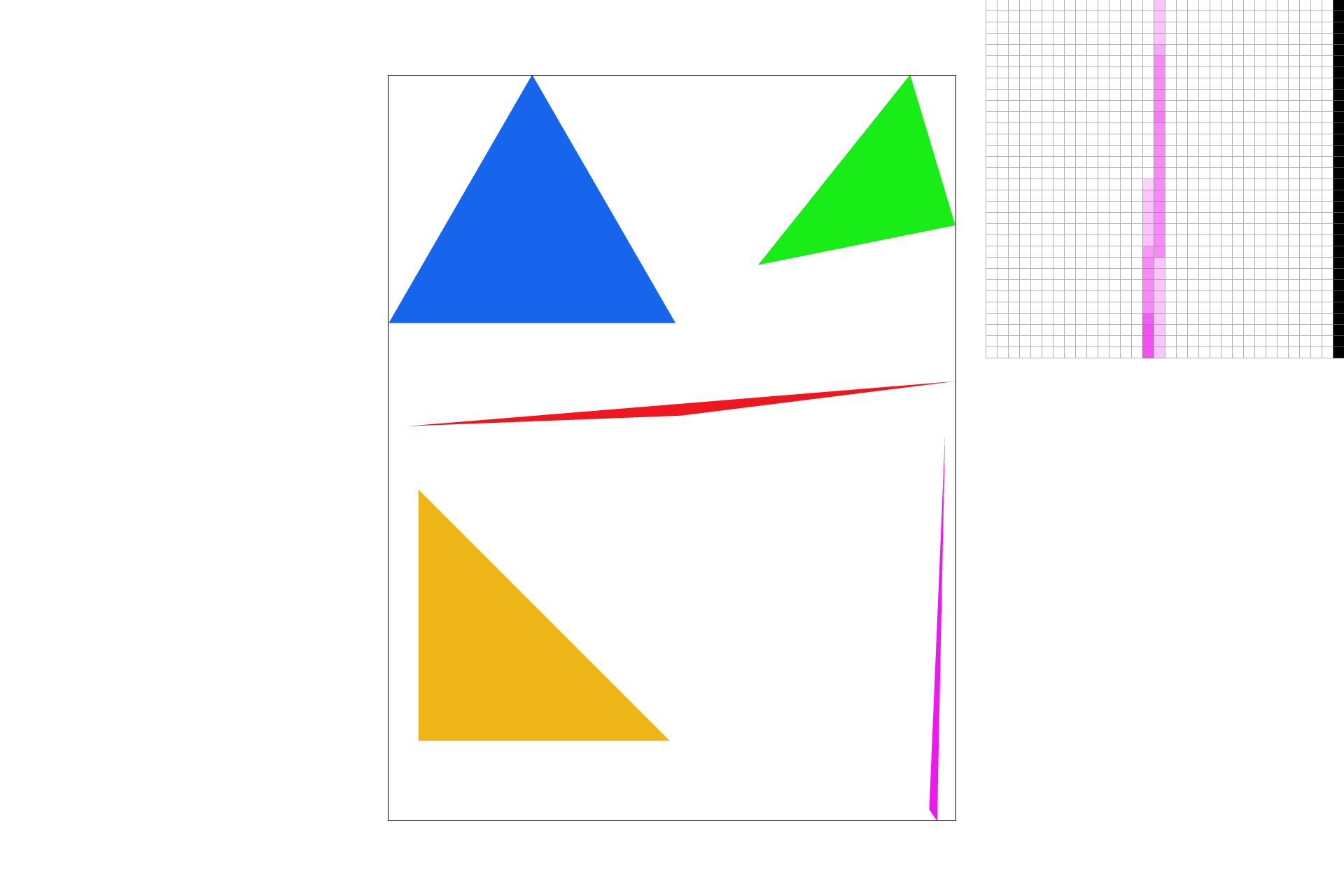
|
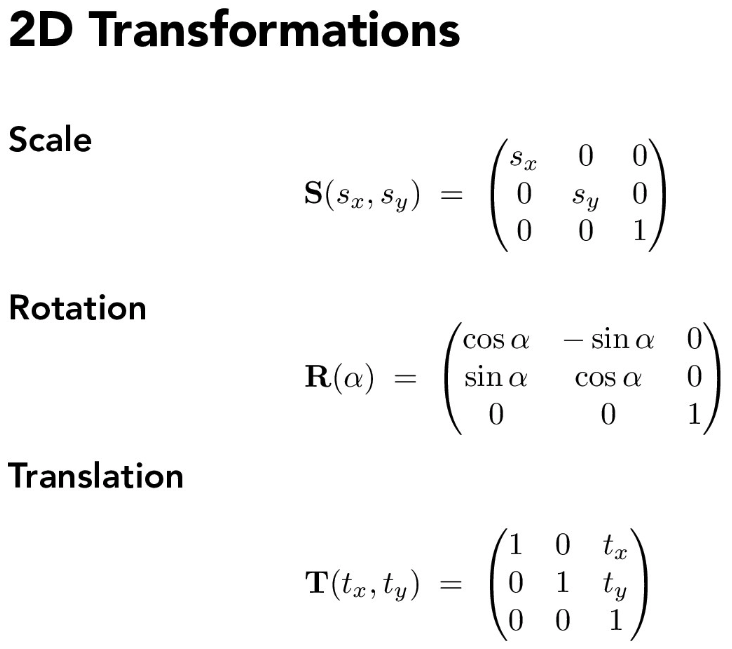
Part 3: Transforms
Implementing transformations was particulary straightforward, the only important part was to identify what the transformation matrices would be.
In my adapted version of the robot, I tried to make him do the wave motion that is often done at sports events by fans in the crowd. I also changed the colors to Blue and Gold to represent either the Golden State Warriors fans or the Golden Bear fans.

Section II: Sampling
Part 4: Barycentric coordinates
Barycentric coordinates are a different way to represent unique points in a triangle as a function of weights of the vertices. The weights typically sum to 1 and are all positive for points inside the triangle.
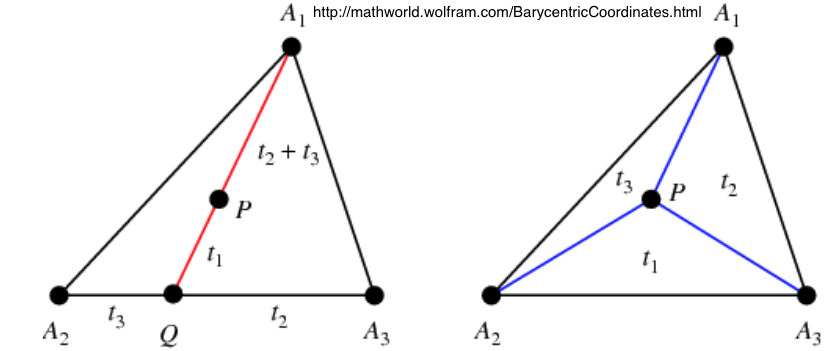
In this section, we built a gradient wheel using barycentric coordinates to obtain samples for color values in the triangle.

Part 5: "Pixel sampling" for texture mapping
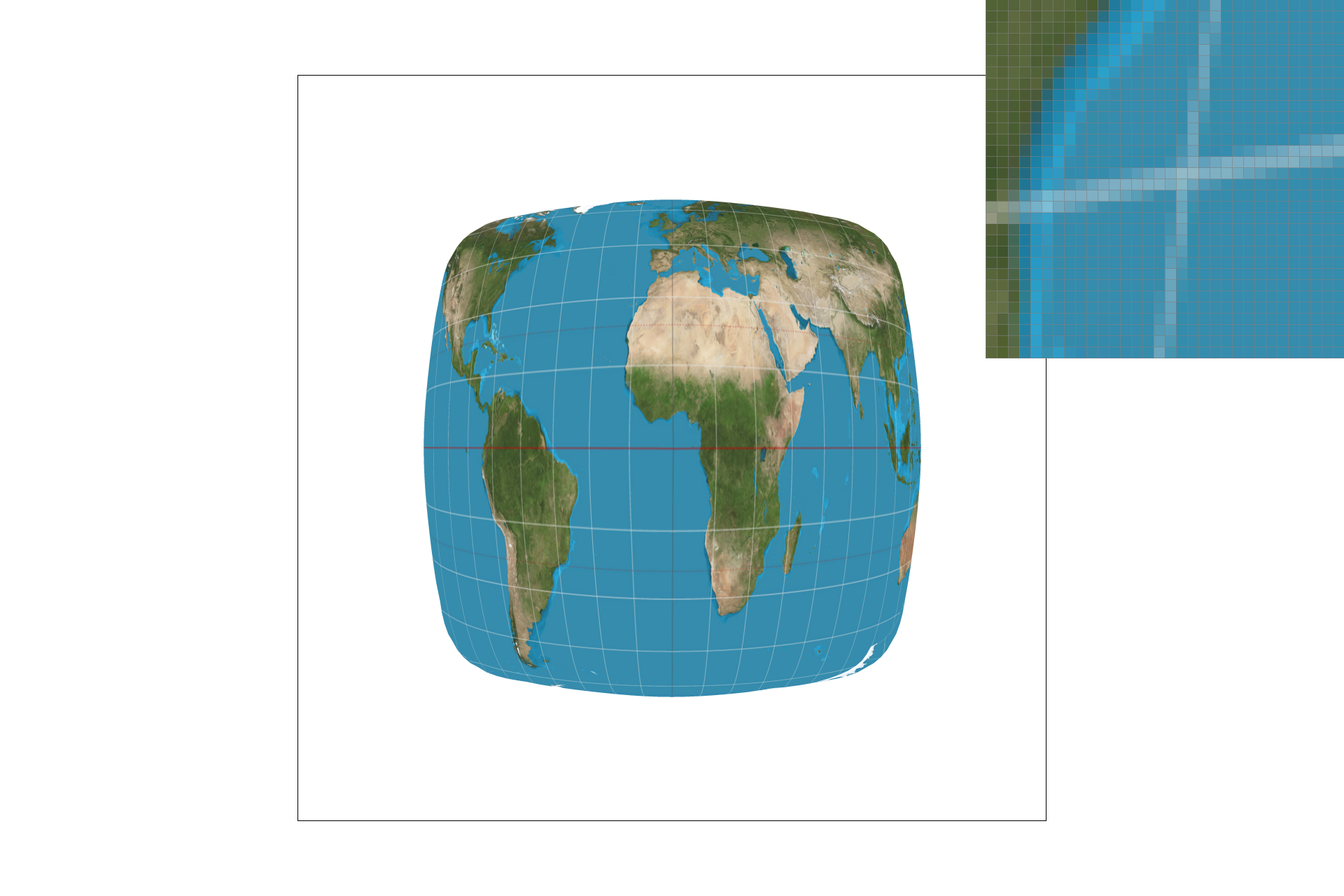
Pixel sampling is how we map textures onto triangles of the vector graphic. We calculate the uv coordinates using the given information about barycentric coordinates and Cartesian coordinates, and then use the uv coordinates to sample the textures and decide what colors to fill into the TexTri triangles to build a textured image. Some samples are shown below.
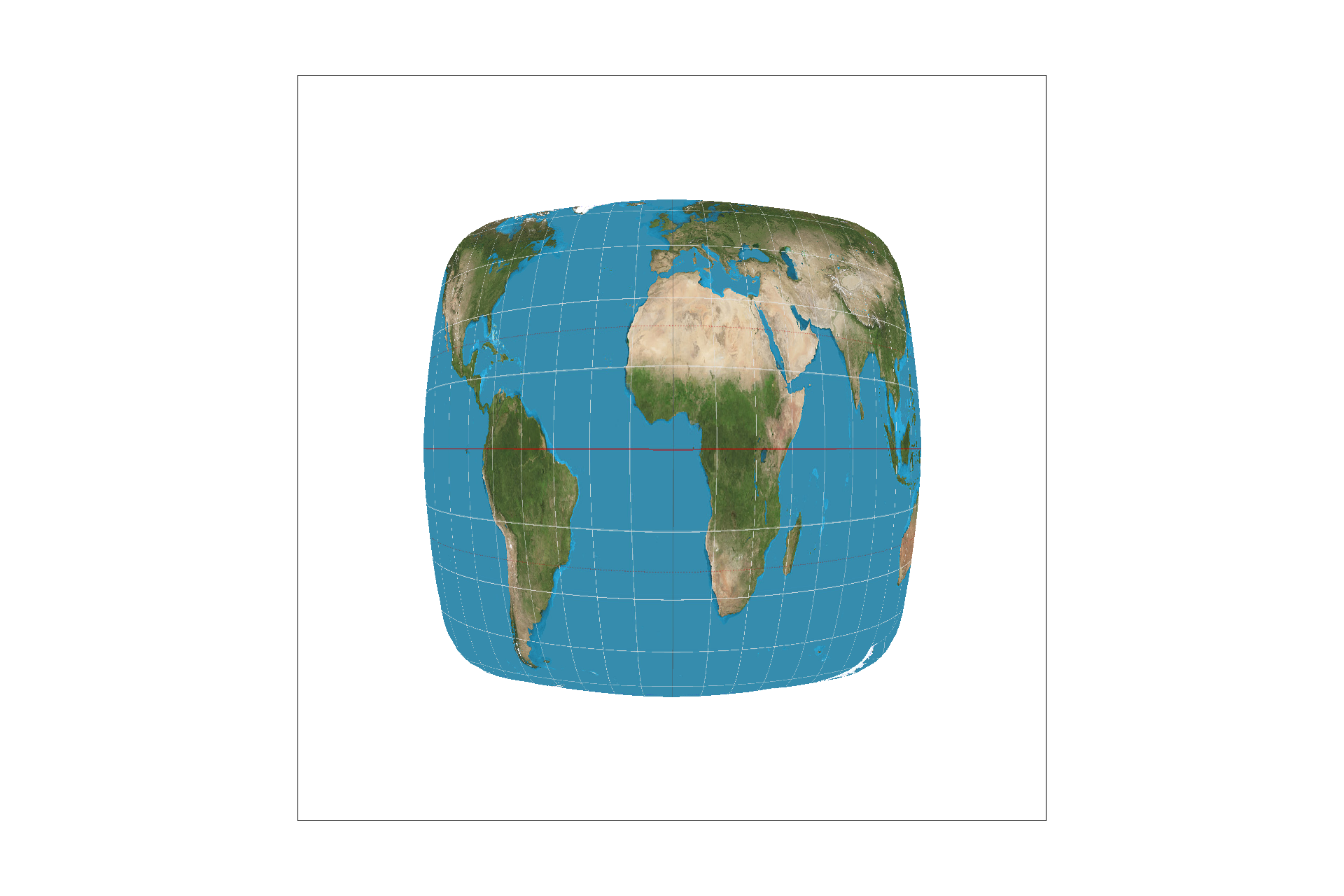
|
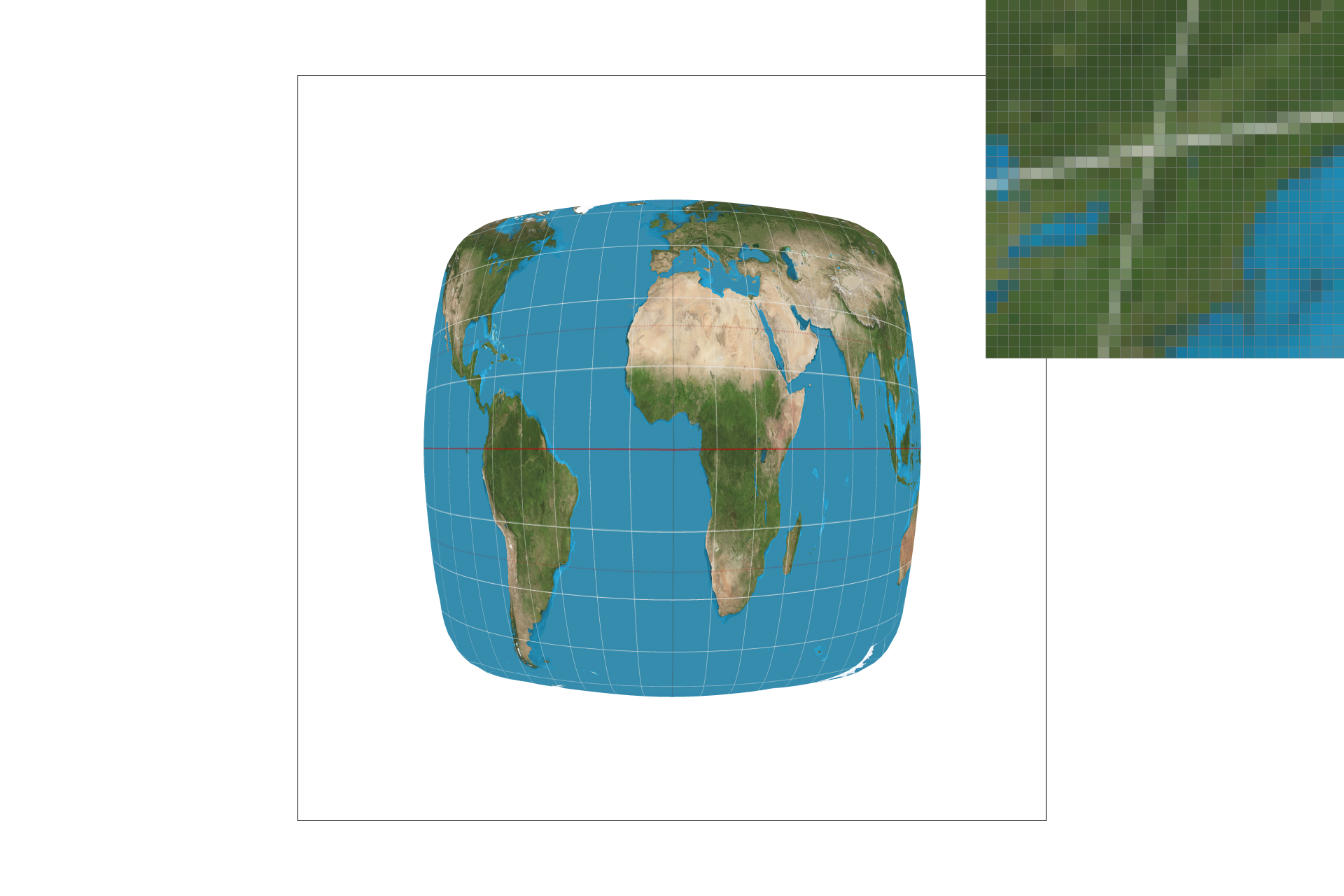
|
|
|
The nearest sample method takes in the calculated uv coordinate points as floats, and takes literally the nearest whole value it can find by rounding to a whole coordinate value so that it can index and obtain a color sample. It uses this to fill the color of the sampled spot. Bilinear on the other hand takes four samples from whole values around the calculated coordinate and averages them to create a weighted sample of neighbors in two linear directions for the new fill value.
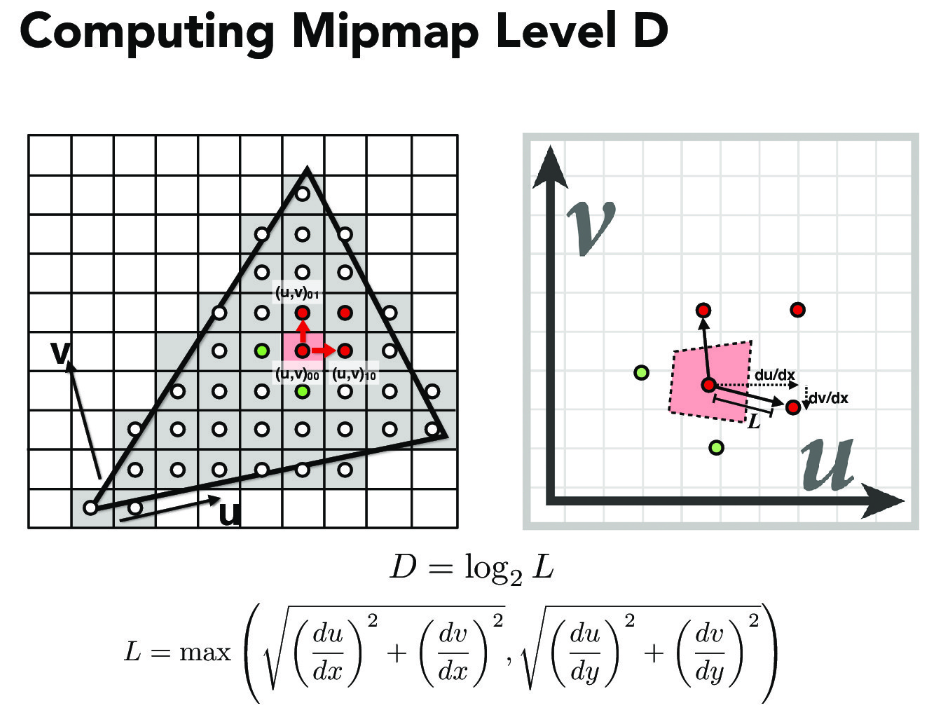
Part 6: "Level sampling" with mipmaps for texture mapping
The mipmap levels were actually one of the hardest parts of the project for me to understand. Even after following the instructions and implementing what I felt was a correct version of the Level Sampling, I still did not quite understand it for a while.
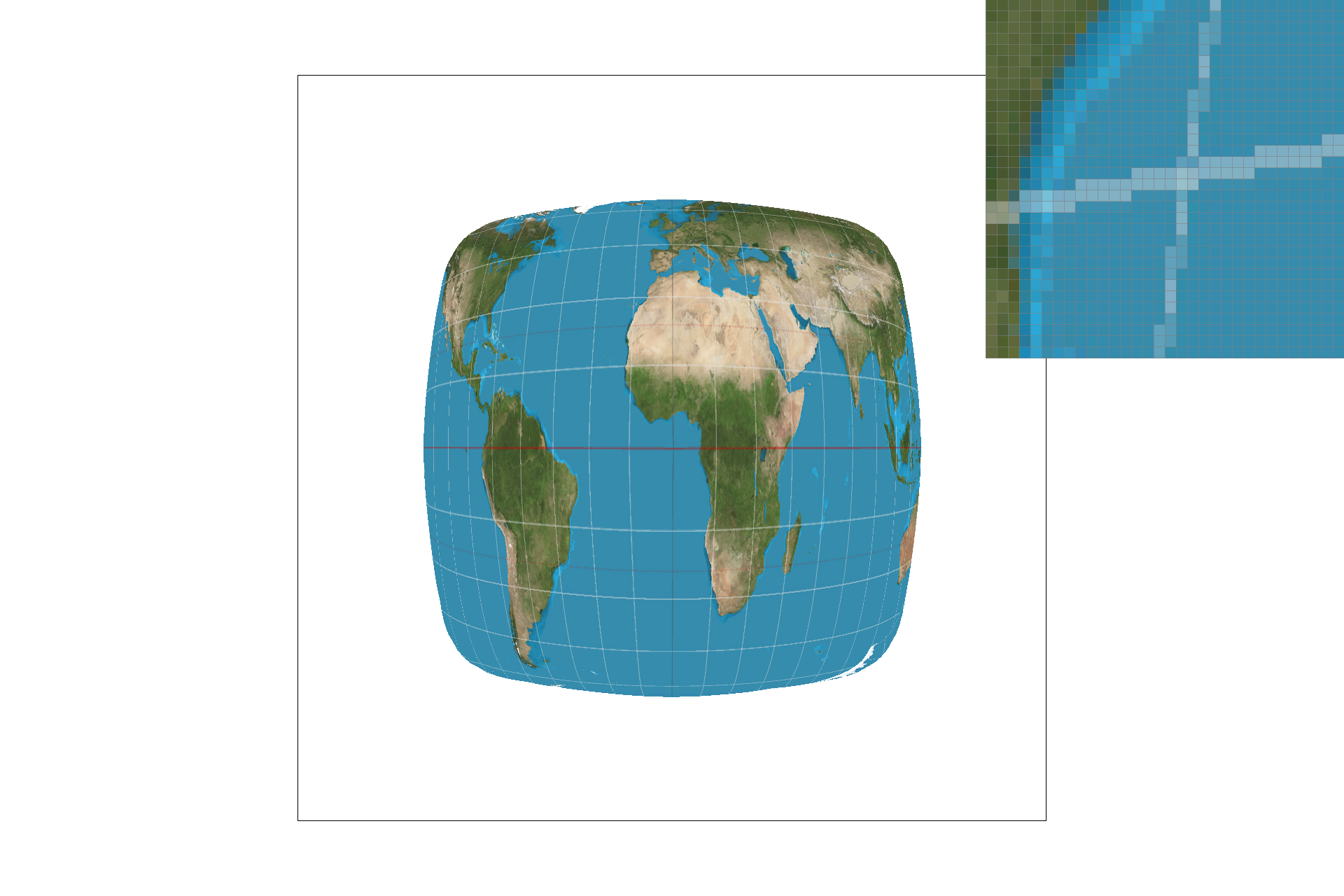
Currently, I understand the mipmap as a form of a low-pass filter to downsample the texture file, store the lower resolutions for each location and use it to downsample or minify the texture scene. the hierarchy follows levels (D) and the storage overhead of the lower resolutions is 4/3 times the orignal size. The overall purpose is to estimate the texture footprint using coordinates of neighboring screen samples.
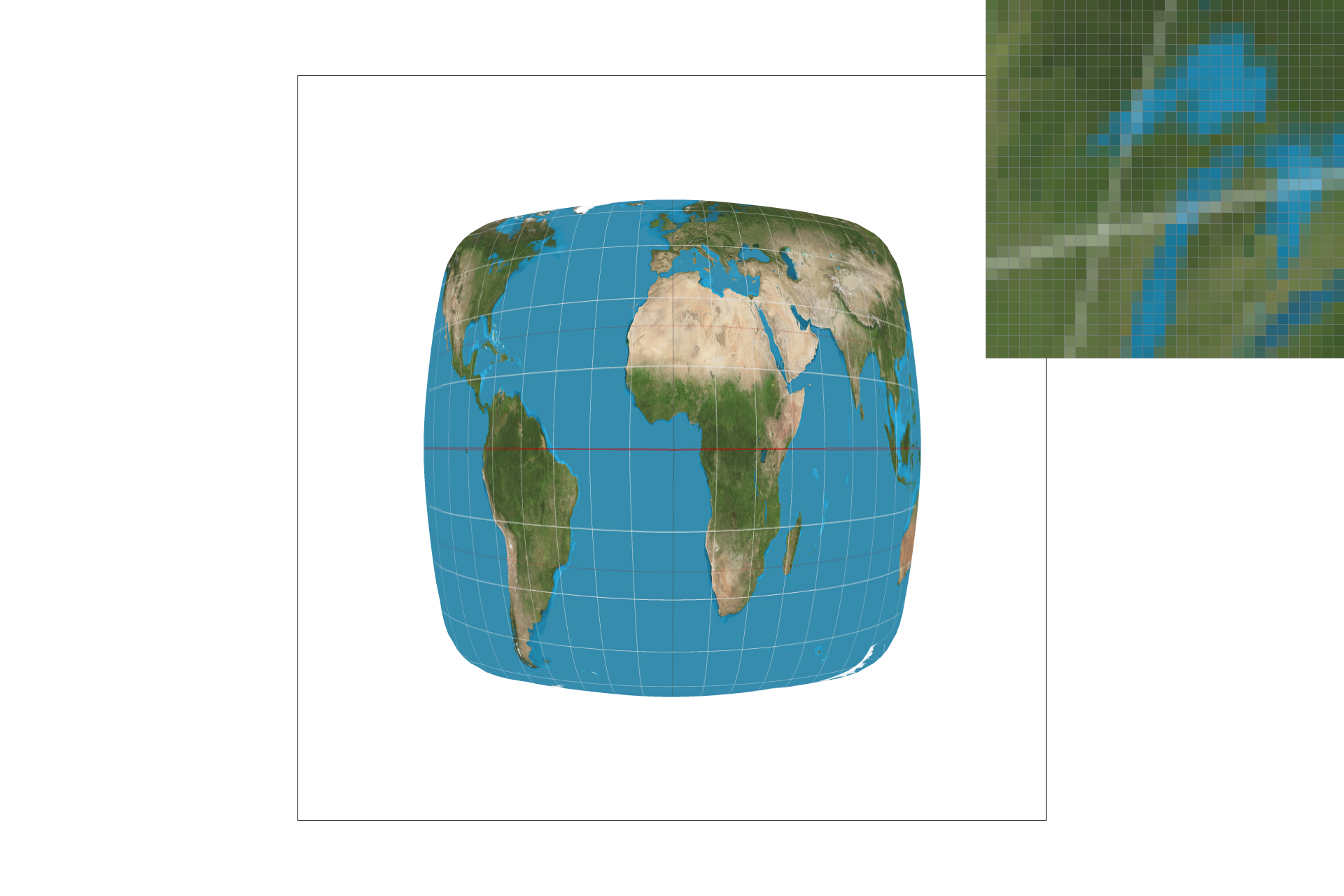
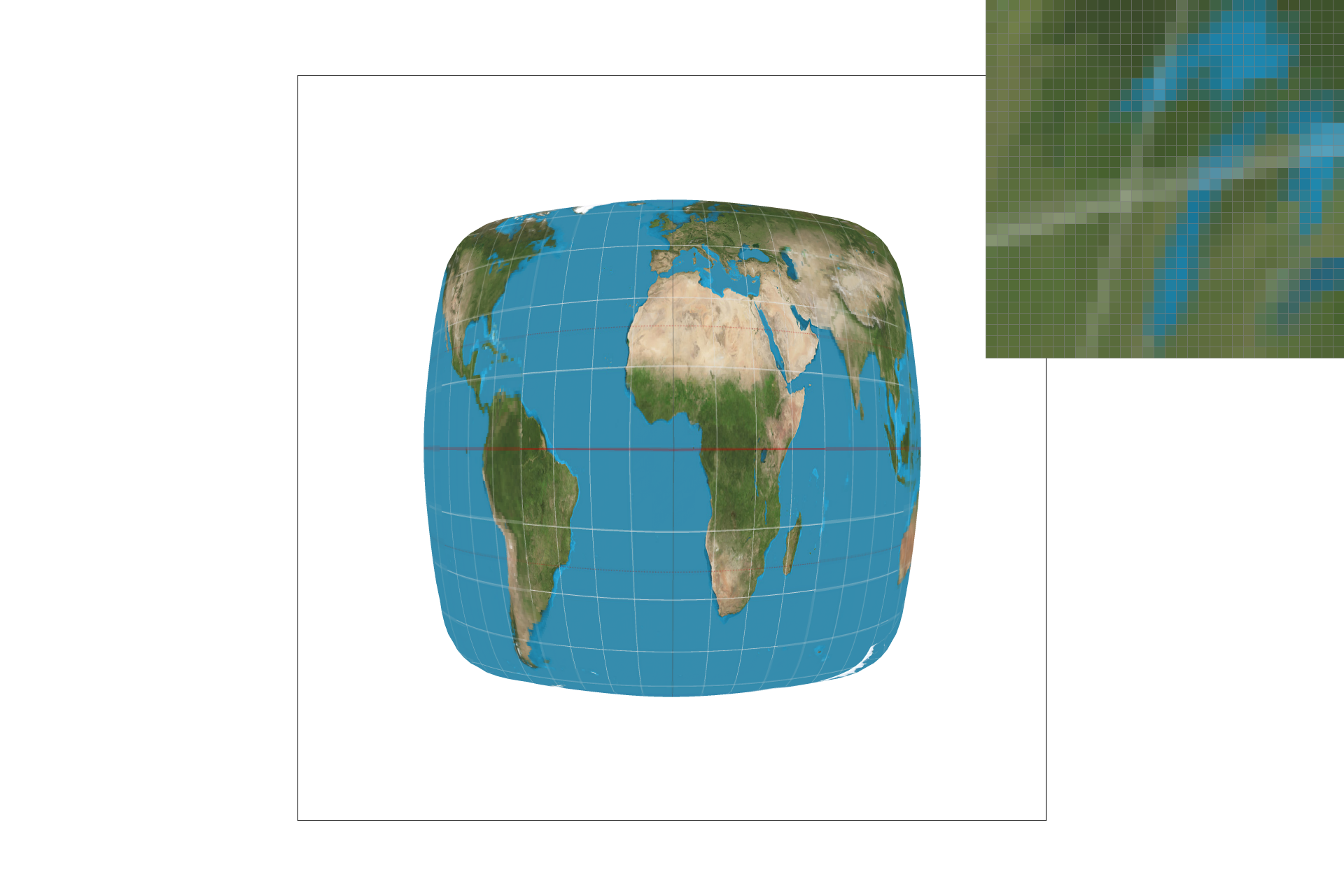
To implement level sampling, I used the formula from the slides and the project spec to compute the appropriate mipmap level to access, then scaled the uv texture coordinates to that level's resolution, and obtained the sample for the texture from that level of the mipmap. There is definitely more blur in the mipmap non-zero level technique, but speed is slightly faster, although it has a 4/3 memory overhead. Some combinations of output are displayed below.
My own SVG

|

|

|

|

|

|
SVG from the Original

|

|

|
|

|
|
Thanks for reading!
